题目内容
20. 如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.∠DCA=40°,
如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.∠DCA=40°,则∠DCB=30°.
分析 根据线段垂直平分线性质求出AD=DC,求出∠A=∠DCA=40°,根据等腰三角形性质和三角形内角和定理求出∠ABC,即可得出答案.
解答 解:∵AC的垂直平分线分别交AB、AC于点D、E,
∴AD=DC,
∵∠DCA=40°,
∴∠A=∠DCA=40°,
∵AB=AC,
∴∠ACB=∠B=$\frac{1}{2}$(180°-∠A)=70°,
∴∠DCB=∠ABC-∠DCA=70°-40°=30°,
故答案为:30.
点评 本题考查了线段垂直平分线性质,三角形内角和定理,等腰三角形的性质的应用,能求出AD=DC和∠ABC的度数是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
11.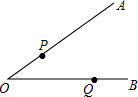 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )| A. | ∠AOB的平分线与PQ的交点 | |
| B. | ∠OPQ与∠OQP的角平分线的交点 | |
| C. | ∠AOB的平分线与线段PQ的垂直平分线的交点 | |
| D. | 线段PQ的垂直平分线与∠OPQ的平分线的交点 |
15.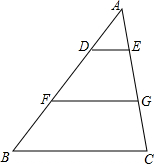 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )| A. | 1:3 | B. | 2:3 | C. | 3:2 | D. | 3:1 |