题目内容
1.当m为何整数时,方程组$\left\{\begin{array}{l}{2x+my=8}\\{x+2y=3}\end{array}\right.$的解是正整数?并求出这时方程的解.分析 先运用列举法确定方程x+2y=3的正整数解,把正整数解代入2x+my=8,求出m的值,解方程组即可.
解答 解:方程x+2y=3的正整数解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
把x=1、y=1代入2x+my=8得,
m=6,
$\left\{\begin{array}{l}{2x+6y=8①}\\{x+2y=3②}\end{array}\right.$,
②×3-①得,x=1,
把x=1代入②得,y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解和方程的知识解的知识,正确根据题意确定一个方程的正整数解是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
11.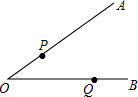 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )| A. | ∠AOB的平分线与PQ的交点 | |
| B. | ∠OPQ与∠OQP的角平分线的交点 | |
| C. | ∠AOB的平分线与线段PQ的垂直平分线的交点 | |
| D. | 线段PQ的垂直平分线与∠OPQ的平分线的交点 |
16.在同一平面内有1998条直线a1,a2,…,a1998,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…那么a1与a1998的位置关系是( )
| A. | 重合 | B. | 平行或重合 | C. | 垂直 | D. | 相交但不垂直 |