题目内容
3. 如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.小明从编号为4的点开始,第三次“移位”后,他到达编号为2的点,第2002次“移位”后,他到达编号为1的点.
如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.小明从编号为4的点开始,第三次“移位”后,他到达编号为2的点,第2002次“移位”后,他到达编号为1的点.
分析 根据移位的定义,结合图形第一次“移位”走4段弧长,然后依次进行计算即可得到第三次“移位”的位置,再根据规律求出第2002次“移位”的位置.
解答 解:从编号为4的点开始,第一次“移位”到达3,
第二次“移位”到达1,
第三次“移位”到达2,
第四次“移位”到达4;
第五次“移位”到达3,
…
依此类推,每4次为一组“移位”循环,
∴2002÷4=500…2,
∴第2002次“移位”后与第2次移位到达的数字编号相同为1.
故答案为:2,1.
点评 此题考查图形的变化规律,读懂题目信息,根据“移位”的定义,找出其变化循环的规律是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
11.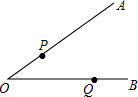 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
 如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )
如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( )| A. | ∠AOB的平分线与PQ的交点 | |
| B. | ∠OPQ与∠OQP的角平分线的交点 | |
| C. | ∠AOB的平分线与线段PQ的垂直平分线的交点 | |
| D. | 线段PQ的垂直平分线与∠OPQ的平分线的交点 |
18. 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )| A. | 变大 | B. | 变小 | C. | 不变 | D. | 不能确定 |
15.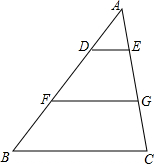 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
 如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )
如图,在△ABC中,DE∥BC,F,G分别为BD,CE的中点.已知BC=8,FG=5,则AD:FB等于( )| A. | 1:3 | B. | 2:3 | C. | 3:2 | D. | 3:1 |
