题目内容
3. 正方形ABCD的边长为1,以CD为直径在正方形内画半圆,再以点C为圆心,1为半径画弧BD,则图中阴影部分的面积为$\frac{π}{8}$.(结果保留π)
正方形ABCD的边长为1,以CD为直径在正方形内画半圆,再以点C为圆心,1为半径画弧BD,则图中阴影部分的面积为$\frac{π}{8}$.(结果保留π)
分析 根据题意有S阴影部分=S扇形BCD-S半圆CD,然后根据扇形的面积公式:S=$\frac{nπR}{360}$和圆的面积公式分别计算扇形和半圆的面积即可.
解答 解:根据题意得,S阴影部分=S扇形BAD-S半圆BA,
∵S扇形BCD=$\frac{90π×{1}^{2}}{360}$=$\frac{π}{4}$,
S半圆CD=$\frac{1}{2}$π($\frac{1}{2}$)2=$\frac{π}{8}$,
∴S阴影部分=$\frac{π}{4}$-$\frac{π}{8}$=$\frac{π}{8}$.
故答案为:$\frac{π}{8}$.
点评 此题考查了扇形的面积公式:S=$\frac{nπR}{360}$,其中n为扇形的圆心角的度数,R为圆的半径),或S=$\frac{1}{2}$lR,l为扇形的弧长,R为半径.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
11. 如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=58°,则∠AED′等于( )
如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=58°,则∠AED′等于( )
 如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=58°,则∠AED′等于( )
如图,把一个矩形纸片ABCD沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=58°,则∠AED′等于( )| A. | 58° | B. | 32° | C. | 122° | D. | 64° |
8.有人预测2014年巴西世界杯足球赛巴西国家队夺冠的概率是85%,下列理解正确的是( )
| A. | 巴西国家队一定夺冠 | B. | 巴西国家队一定不会夺冠 | ||
| C. | 巴西国家队夺冠的可能性比较大 | D. | 巴西国家队夺冠的可能性比较小 |
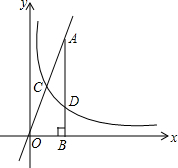 如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第4个正方形的边长为$\frac{27}{8}$$\sqrt{5}$.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第4个正方形的边长为$\frac{27}{8}$$\sqrt{5}$.