题目内容
15. 如图,AC,BD相交于O,∠A=∠D,AB=DC.
如图,AC,BD相交于O,∠A=∠D,AB=DC.求证:AC=BD.
分析 证明△ABO≌△DCO(AAS),得到OA=OD,OB=OC,所以OA+OC=OD+OB,即AC=BD.
解答 解:在△ABO和△DCO中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AOB=∠DOC}\\{AB=DC}\end{array}\right.$
∴△ABO≌△DCO(AAS),
∴OA=OD,OB=OC,
∴OA+OC=OD+OB,
∴AC=BD.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△ABO≌△DCO.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
5. 如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=( )
如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=( )
 如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=( )
如图,l∥m,等边△ABC的顶点A、B分别在直线l、m上,∠1=25°,则∠2=( )| A. | 35° | B. | 45° | C. | 55° | D. | 75° |
20.下列各式计算中,①-(-2);②-|-2|;③-22;④-(-2)2,⑤(-3×2)2,计算结果为负数的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.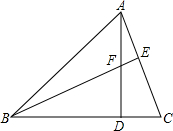 如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为( )
如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为( )
 如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为( )
如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为( )| A. | 60° | B. | 65° | C. | 75° | D. | 80° |
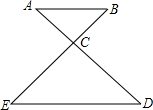 如图:已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=3cm,BC=4cm,CE=6cm.求:
如图:已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=3cm,BC=4cm,CE=6cm.求: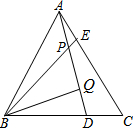 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1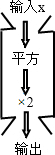 如图是一组数值转换机,若它输出的结果为18,则输入值为±3.
如图是一组数值转换机,若它输出的结果为18,则输入值为±3. 如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等.
如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等.