题目内容
13．
如图，已知四边形ABCD是正方形，则正方形ABCD的面积是（ ）| A． | 25 | B． | 15 | C． | 12.5 | D． | 5 |
分析 在Rt△DCE中，求出DC即可解决问题．
解答 解：∵四边形ABCD是正方形，
∴∠DCB=∠DCE=90°，
∵∠E=45°，
∴∠E=∠CDE=45°，
∵DE=5，
∴CD=CE=$\frac{5\sqrt{2}}{2}$，
∴正方形ABCD的面积=（$\frac{5\sqrt{2}}{2}$）2=12.5，
故选C．
点评 本题考查正方形的性质、等腰直角三角形的判定和性质等知识，解题的关键是熟练掌握等腰直角三角形的性质，求出DC是突破点，属于中考基础题．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
12．$\sqrt{13}$≈3.61，$\sqrt{1.3}$≈1.14，则$\sqrt{13000}$≈（ ）
| A． | 36.1 | B． | 11.4 | C． | 361 | D． | 114 |
4．一个人从A地出发向北偏东80°方向到达B地，再从B地向北偏西25°方向到达C地，如果∠ACB=55°，则∠CAB的度数是（ ）
| A． | 25° | B． | 50° | C． | 70° | D． | 75° |
1．如（2x+m）与（4x+3）的乘积中不含x的一次项，则m的值为（ ）
| A． | -$\frac{3}{2}$ | B． | $\frac{3}{2}$ | C． | -$\frac{2}{3}$ | D． | $\frac{2}{3}$ |
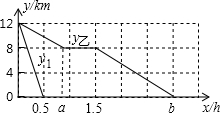某景区内从甲地到乙地的路程是12km，小华步行从甲地到乙地游玩，速度为5km/h，走了4km后，中途休息了一段时间，然后继续按原速前往乙地，景区从甲地开往乙地的电瓶车每隔半小时发一趟车，速度是24km/h，若小华与第1趟电瓶车同时出发，设小华距乙地的路程为y乙（km），第n趟电瓶车距乙地的路程为yn（km），n为正整数，行进时间为x（h）．如图画出了y乙，y1与x的函数图象．
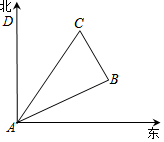如图所示，在一次夏令营活动中，小明从营地A点出发，沿北偏东60°方向走了5$\sqrt{3}$km到达B点，然后再沿北偏西30°方向走了5km到达目的地C点．
5．已知一个等腰三角形一边长为4cm，另一边长为6cm，那么这个等腰三角形的周长为（ ）
| A． | 14cm | B． | 16cm | C． | 14cm或16cm | D． | 以上都不对 |