题目内容
18.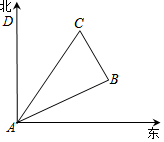 如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了5$\sqrt{3}$km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了5$\sqrt{3}$km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
分析 (1)根据平行线的性质,可得∠ABF,根据直角三角形的判定,可得∠ABC,根据勾股定理,可得答案;
(2)根据直角三角形的性质,可得∠CAB,根据角的和差,可得答案.
解答 解:(1)过B点作直线EF∥AD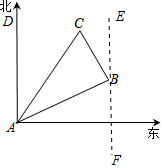 ,
,
∴∠DAB=∠ABF=60°,
∵∠EBC=30°,
∴∠ABC=180°-∠ABF-∠EBC=180°-60°-30°=90°,
∴△ABC为直角三角形,由已知可得:BC=5km,AB=5$\sqrt{3}$km,
由勾股定理可得:AC2=BC2+AB2,
所以AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=10(km),
即:A、C两点之间的距离为10km;
(2)在Rt△ABC中,∵BC=5km,AC=10km,
∴∠CAB=30°,
∵∠DAB=60°,
∴∠DAC=30°,
即点C在点A的北偏东30°的方向上.
点评 本题考查了勾股定理的应用,利用了方向角,平行线的性质,直角三角形的性质,勾股定理.

练习册系列答案
相关题目
9.从-3,1,-2这三个数中,任选两个数的积作为k的值,则使正比例函数y=kx的图象经过第二、四象限的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
6.将某图形的各顶点的横坐标减去2,纵坐标保持不变,可将该图形( )
| A. | 向右平移2个单位 | B. | 向左平移2个单位 | C. | 向上平移2个单位 | D. | 向下平移2个单位 |
13. 如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )
如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )
 如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )
如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )| A. | 25 | B. | 15 | C. | 12.5 | D. | 5 |
3.下面的四个图形中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
10.已知ax=3,ay=5,则ax+y的值为( )
| A. | 8 | B. | 35 | C. | 15 | D. | 53 |
8.-27的立方根与9的平方根之和是( )
| A. | 0 | B. | 6 | C. | 0或-6 | D. | -12或6 |
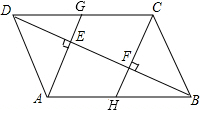 如图,在?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点G、H.
如图,在?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点G、H.