题目内容
1.如(2x+m)与(4x+3)的乘积中不含x的一次项,则m的值为( )| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
分析 先根据已知式子,可找出所有含x的项,合并系数,令含x项的系数等于0,即可求m的值.
解答 解:(2x+m)(4x+3)=8x2+(4m+6)x+3m,
∵乘积中不含x的一次项,
∴4m+6=0,
∴m=-$\frac{3}{2}$.
故选:A.
点评 本题主要考查多项式乘以多项式的法则,注意不含某一项就是说含此项的系数等于0.

练习册系列答案
相关题目
9.从-3,1,-2这三个数中,任选两个数的积作为k的值,则使正比例函数y=kx的图象经过第二、四象限的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
6.将某图形的各顶点的横坐标减去2,纵坐标保持不变,可将该图形( )
| A. | 向右平移2个单位 | B. | 向左平移2个单位 | C. | 向上平移2个单位 | D. | 向下平移2个单位 |
13. 如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )
如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )
 如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )
如图,已知四边形ABCD是正方形,则正方形ABCD的面积是( )| A. | 25 | B. | 15 | C. | 12.5 | D. | 5 |
10.已知ax=3,ay=5,则ax+y的值为( )
| A. | 8 | B. | 35 | C. | 15 | D. | 53 |
 如图:直线AB,CD交于O点,OE平分∠AOC,若∠1=30°,则∠AOD=120°.
如图:直线AB,CD交于O点,OE平分∠AOC,若∠1=30°,则∠AOD=120°.
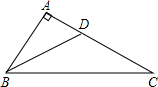 在△ABC中,∠A=90°,BD是△ABC的角平分线,AB=8cm,BD=10cm,则点D到BC的距离为6cm.
在△ABC中,∠A=90°,BD是△ABC的角平分线,AB=8cm,BD=10cm,则点D到BC的距离为6cm.