题目内容
 如图,矩形ABDE中,C为BD上一动点,作CF⊥AC交AE所在的直线于F,若AB=4,求AF的最小值.
如图,矩形ABDE中,C为BD上一动点,作CF⊥AC交AE所在的直线于F,若AB=4,求AF的最小值.考点:矩形的性质,勾股定理,等腰直角三角形
专题:
分析:根据(a-b)2≥0,即a2+b2≥2ab,(当a=b时等号成立),那么在直角三角形ACF中AF=
≥
,(当AC=CF是等号成立),则AF的最小值=
=
AC,从而得出△ACF是等腰直角三角形,进而得出△ABC是等腰直角三角形,从而求得AC的值,即可求得AF的最小值.
| AC2+CF2 |
| 2AC•CF |
| 2AC•CF |
| 2 |
解答:解:∵(a-b)2≥0,即a2+b2≥2ab,(当a=b时等号成立)
∵CF⊥AC,
∴AF=
≥
,(当AC=CF是等号成立)
∴AF的最小值=
=
AC,
此时△ACF是等腰直角三角形,
∴∠CAF=45°,
∴∠BAC=45°,
∴△ABC是等腰直角三角形,
∴AC=
AB=4
∴AF的最小值=
AC=
×4
=8.
∵CF⊥AC,
∴AF=
| AC2+CF2 |
| 2AC•CF |
∴AF的最小值=
| 2AC•CF |
| 2 |
此时△ACF是等腰直角三角形,
∴∠CAF=45°,
∴∠BAC=45°,
∴△ABC是等腰直角三角形,
∴AC=
| 2 |
| 2 |
∴AF的最小值=
| 2 |
| 2 |
| 2 |
点评:本题考查了矩形的性质,勾股定理的应用,等腰直角三角形的判定和性质,根据(a-b)2≥0,即a2+b2≥2ab,(当a=b时等号成立),是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在矩形ABCD中,AB=24cm,BC=12cm.点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤12).
如图,在矩形ABCD中,AB=24cm,BC=12cm.点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤12).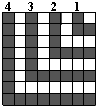 如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成.图中,第1个黑色形由3个正方形组成,第2个黑色形由7个正方形组成,那么组成第12个黑色形的正方形个数是( )
如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成.图中,第1个黑色形由3个正方形组成,第2个黑色形由7个正方形组成,那么组成第12个黑色形的正方形个数是( )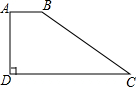 如图,在直角梯形ABCD中,AB∥DC,AD⊥CD于点D,若AB=1,AD=2,DC=4,则BC的长为
如图,在直角梯形ABCD中,AB∥DC,AD⊥CD于点D,若AB=1,AD=2,DC=4,则BC的长为