Question

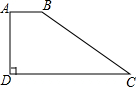如图，在直角梯形ABCD中，AB∥DC，AD⊥CD于点D，若AB=1，AD=2，DC=4，则BC的长为

 

．

Answer 1

考点：直角梯形

专题：

分析：过B作BE⊥CD交CD于点E，由题意可知AD∥BE且AD=BE=2，AB=DE=1，可得CE=DC-DE=3，在直角三角形BED中，根据勾股定理即可求得BC的长．

解答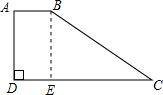：解：如图，过B作BE⊥DC于点E，
∵AB∥CD，AD⊥CD，BE⊥CD，
∴AB=DE=2，AB=DE=1；
∴EC=DC-DE=4-1=3；
在直角三角形BEC中，∠BEC=90°，
∴BC=

BE2+CE2

=

22+32

=

13

．
故答案为：

13

．

点评：考查了直角梯形，本题解题的关键在于作辅助线，构造直角三角形，通过解直角三角形即可得解．此题涉及到直角梯形、矩形的性质及勾股定理的运用，是一道较简单的综合题型．