题目内容
20.已知直线y=-$\frac{3}{4}$x+6和直线y=$\frac{3}{4}$x-2相交于点P,且直线y=-$\frac{3}{4}$x+6分别交x轴、y轴于点A、B,直线y=$\frac{3}{4}$x-2交y轴于点C,则点A的坐标为(8,0),点P的坐标为($\frac{16}{3}$,2).分析 (1)直线y=-$\frac{3}{4}$x+6,求出当y=0时x的值即可;
(2)解方程组即可得到结论.
解答 解:∵直线y=-$\frac{3}{4}$x+6分别交x轴、y轴于点A、B,
∴当y=0时,-$\frac{3}{4}$x+6=0,
交解得:x=8,
∴A(8,0);
解方程组$\left\{\begin{array}{l}{y=-\frac{3}{4}x+6}\\{y=\frac{3}{4}x-2}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{16}{3}}\\{y=2}\end{array}\right.$,
∴P($\frac{16}{3}$,2);
故答案为:(8,0);($\frac{16}{3}$,2).
点评 本题考查了两直线相交的问题,两函数解析式求交点坐标;熟练掌握两条直线交点坐标的求法是关键.

练习册系列答案
相关题目
8.已知一次函数y=(m-1)x+m的图象分别交x轴负半轴、y轴负半轴于点A、B,则m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m<0 | D. | m>0 |
12.不等式-3x+2>-4的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |




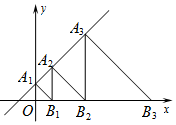 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2、点A3…在直线l上,分别过点点A2、点A3…作点A2B1⊥x轴于点B1,A3B2⊥x轴于点B2…,若A1B1∥A2B2∥A3B3…,OB1=2,则线段AnBn的长为2n$•\sqrt{2}$.
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2、点A3…在直线l上,分别过点点A2、点A3…作点A2B1⊥x轴于点B1,A3B2⊥x轴于点B2…,若A1B1∥A2B2∥A3B3…,OB1=2,则线段AnBn的长为2n$•\sqrt{2}$.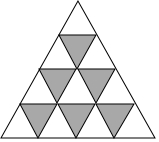 如图是由若干个全等的等边三角形拼成的纸板,某人向纸板上投掷飞镖(每次飞镖均落在纸板上),飞镖落在阴影部分的概率是$\frac{3}{8}$.
如图是由若干个全等的等边三角形拼成的纸板,某人向纸板上投掷飞镖(每次飞镖均落在纸板上),飞镖落在阴影部分的概率是$\frac{3}{8}$.