题目内容
8.已知一次函数y=(m-1)x+m的图象分别交x轴负半轴、y轴负半轴于点A、B,则m的取值范围是( )| A. | m>1 | B. | m<1 | C. | m<0 | D. | m>0 |
分析 先判断一次函数y=(m-1)x+m的图象经过第二、三、四象限,再根据一次函数与系数的关系得到m-1<0且m<0,然后求出两个不等式的公共部分即可.
解答 解:∵一次函数y=(m-1)x+m的图象分别交x轴负半轴、y轴负半轴于点A、B,
即一次函数y=(m-1)x+m的图象经过第二、三、四象限,
∴m-1<0且m<0,
∴m的取值范围是m<0.
故选C.
点评 本题考查了一次函数与系数的关系:对于一次函数y=kx+b,它与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.当k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
相关题目
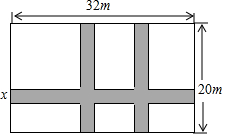 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2,则道路宽x为1m.
如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2,则道路宽x为1m.