题目内容
9．
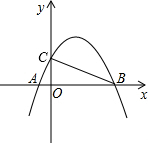如图，抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C（0，2），且OB=4OA，tan∠OCB=2，求抛物线的解析式．
分析 利用已知结合锐角三角函数定义得出A，B，点坐标，进而利用交点式求出二次函数解析式．
解答 解：∵点C（0，2），
∴CO=2，
∵tan∠OCB=2，
∴BO=4，B（4，0），
∵OB=4OA，
∴AO=1，
∴A（-1，0），
设抛物线解析式为：y=a（x+1）（x-4），
将（0，2）代入得：
2=-4a，
解得：a=-$\frac{1}{2}$，
故抛物线的解析式为：y=-$\frac{1}{2}$（x+1）（x-4）．
点评 此题主要考查了抛物线与x轴的交点以及二次函数解析式求法，正确得出A，B点坐标是解题关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
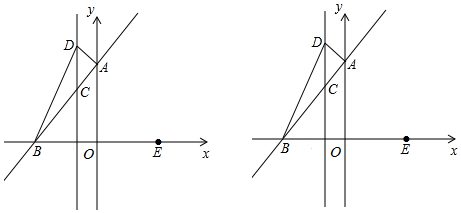
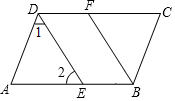如图，∠CDA=∠CBA，DE平分∠CDA，BF平分∠CBA，且∠1=∠2，试说明DE∥FB．
如图，∠B与∠BCD互为余角，∠B=∠ACD，DE⊥BC，垂足为E，AC与DE平行吗？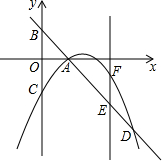
如图，在平面直角坐标中，直线y=-x+2交x轴于点A，交y轴于点B，过点A的抛物线y=ax2+bx-2与y轴交于点C，与直线AB的另一个交点为D，点E是射线BA上一点（不与点A、B重合），点F在抛物线上，且EF∥y轴，设点E的横坐标为m．
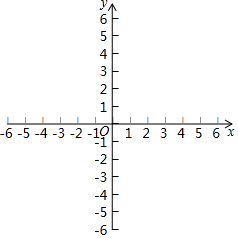观察：点…A（-5，-2）、B（-4，-1），C（1，4）、D（2，5）、E（x，y）…；
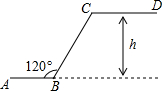如图是某商场一楼与二楼之间手扶电梯示意图，其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=120°，BC的长是8m，则乘电梯从点B到点C上升的高度h是4$\sqrt{3}$m．