题目内容
20.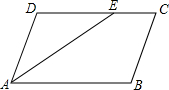 如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.
如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD,AB于E,F.(1)作∠BCD的角平分线CF(尺规作图,保留痕迹,不写作法);
(2)求证:AE=CF.
分析 (1)首先以B为圆心,以任意长为半径化弧,分别与AB,BC的交于点M,N,再分别以M,N为圆心,大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,作射线BP,交CD于点F,则BF即为所求;
(2)由?ABCD中,AE平分∠BAD,CF平分∠BCD,易得AD=BC,∠D=∠B,∠DAB=∠DCB,∠DAE=∠BCF,继而证得△DAE≌△BCF,则可证得结论.
解答  解:(1)如图;①以B为圆心,以任意长为半径化弧,分别与AB,BC的交于点M,N,
解:(1)如图;①以B为圆心,以任意长为半径化弧,分别与AB,BC的交于点M,N,
②分别以M,N为圆心,大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,
③作射线BP,交CD于点F,则BF即为所求
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠DAB=∠DCB,
又∵AE平分∠BAD,CF平分∠BCD,
∴$∠DAE=\frac{1}{2}∠DAB$,$∠BCF=\frac{1}{2}∠DCB$,
∴∠DAE=∠BCF,
在△DAE和△BCF中,
$\left\{\begin{array}{l}∠D=∠B\\ DA=BC\\∠DAE=∠BCF\end{array}\right.$,
∴△DAE≌△BCF(ASA),
∴AE=CF.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△DAE≌△BCF是关键.

练习册系列答案
相关题目
15.下列运算中正确的是( )
| A. | 3a+2a=5a2 | B. | (2a2)3=8a6 | C. | 2a2•a3=2a6 | D. | (2a+b)2=4a2+b2 |
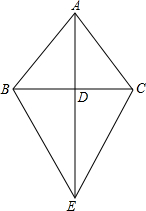 如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论.
如图,△ABC中,AB=AC,AD⊥BD于点D,E是AD延长线上的一点,且BC=BE,请判断△BCE的形状,并证明你的结论. 如图,点E是平行四边形ABCD边BC上的一点,连接AC,DE,且AB=AE.
如图,点E是平行四边形ABCD边BC上的一点,连接AC,DE,且AB=AE. 如图,已知AB∥CD,∠1=150°,则∠2=30°.
如图,已知AB∥CD,∠1=150°,则∠2=30°. 如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD,求证:直线PD是⊙O的切线.
如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD,求证:直线PD是⊙O的切线.