题目内容
已知P为⊙O外一点，PA切⊙O于点A，PO交⊙O于点B，若PA=6，BP=4，那么⊙O的半径为________．
2.5
分析：设圆O半径为r，PA切⊙O于点A，利用切割线定理可得PA2=BP•PD，列方程62=4×（4+2r）解方程即可求解．
解答：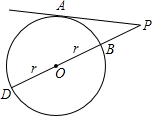
解：如图：
设圆O半径为r，PA切⊙O于点A，
则PA2=BP•PD，
即62=4×（4+2r），
r=2.5，
故⊙O的半径为2.5．
点评：解答本题关键是延长PB，根据切割线定理解答．
分析：设圆O半径为r，PA切⊙O于点A，利用切割线定理可得PA2=BP•PD，列方程62=4×（4+2r）解方程即可求解．
解答：
解：如图：设圆O半径为r，PA切⊙O于点A，
则PA2=BP•PD，
即62=4×（4+2r），
r=2.5，
故⊙O的半径为2.5．
点评：解答本题关键是延长PB，根据切割线定理解答．
练习册系列答案
相关题目
如图，已知P为⊙O外一点，PO交⊙O于点A，割线PBC交⊙O于点B、C，且PB=BC，若OA=7，PA=4，则PB的长等于（ ）A、6
| ||
B、
| ||
| C、6 | ||
D、2
|
已知P为⊙O外一点，PA，PB为⊙O的切线，A、B为切点，∠P=70°，C为⊙O上一个动点，且不与A、B重合，则∠BCA=（ ）
| A、35°、145° | B、110°、70° | C、55°、125° | D、110° |
如图，已知A为⊙O外一点，连接OA交⊙O于P，AB切⊙O于B，AP=6cm，AB=
如图，已知P为⊙O外一点，PA，PB分别切⊙O于点A，B，BC为直径．求证：AC∥OP．
如图，已知F为△ABC外一点，点D、E分别在边AB、AC上，且