题目内容
5.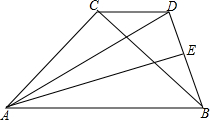 如图,点C在线段AB的垂直平分线上,且AC⊥BC,CD∥AB,AB=AD,点E为BD的中点.求证:AE、AD三等分∠BAC.
如图,点C在线段AB的垂直平分线上,且AC⊥BC,CD∥AB,AB=AD,点E为BD的中点.求证:AE、AD三等分∠BAC.
分析 过C作CH⊥AB于H,过A作AF⊥DC交DC延长线于F,求出四边形AFCH是矩形,根据矩形的性质得出CF=AH,AF=CH,根据线段垂直平分线的性质求出AC=BC,求出AF=FC=AH=CH=$\frac{1}{2}$AB=$\frac{1}{2}$AD,根据含30°角的直角三角形性质求出∠FDA=30°,∠FAD=60°,求出∠CAD=15°,根据等腰三角形性质求出∠DAE=∠BAE=15°,即可得出答案.
解答 证明:如图: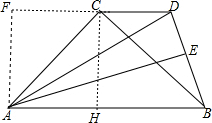
过C作CH⊥AB于H,过A作AF⊥DC交DC延长线于F,
则∠F=∠AHB=90°,
∵CD∥AB,
∴∠FAH=∠F=∠CHA=90°,
∴四边形AFCH是矩形,
∴CF=AH,AF=CH,
∵C在AB垂直平分线上,
∴AC=BC,
∵AC⊥BC,
∴∠ACB=90°,
∴∠CBA=∠CAB=45°,
∴∠FAC=90°-45°=45°,
∴∠FCA=∠FAC=45°,
∴AF=FC=AH=CH=$\frac{1}{2}$AB,
∵AD=AB,
∴AF=$\frac{1}{2}$AD,
∵∠F=90°,
∴∠FDA=30°,∠FAD=60°,
∴∠CAD=60°-45°=15°,
∵AD=AB,E为BD的中点,
∴∠DAE=∠BAE=$\frac{1}{2}$(45°-15°)=15°,
即∠CAD=∠DAE=∠BAE=15°,
所以AE、AD三等分∠BAC.
点评 本题考查了矩形的性质和判定,等腰直角三角形,线段垂直平分线性质,等腰三角形的性质,含30°角的直角三角形性质的应用,能综合运用定理进行推理是解此题的关键,题目综合性比较强,难度偏大.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
15. 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )| A. | 2015 | B. | 2016 | C. | $\sqrt{2015}$ | D. | $\sqrt{2016}$ |
16.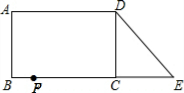 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.
已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时.△ABP和△DCE全等.| A. | 1 | B. | 1或3 | C. | 1或7 | D. | 3或7 |
13.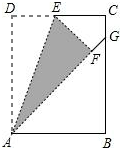 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{3}$ |
20.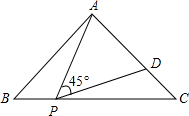 如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
 如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )
如图,等腰直角△ABC的直角边长为3,P为斜边BC上的一点,且BP=1,D为AC上一点,若∠APD=45度,则以PA为边的正方形的面积为( )| A. | 10-3$\sqrt{2}$ | B. | 10-2$\sqrt{3}$ | C. | 4 | D. | 6 |
 已知:如图,在四边形ABCD中,AB=3,BC=12,CD=8,AD=4,BD=6,求证:BD平分∠ABC.
已知:如图,在四边形ABCD中,AB=3,BC=12,CD=8,AD=4,BD=6,求证:BD平分∠ABC.