题目内容
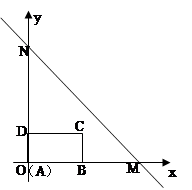
如图,直线 :
: 与
与 轴交于点
轴交于点 (4,0),与
(4,0),与 轴交于点
轴交于点 ,长方形
,长方形 的边
的边 在
在 轴上,
轴上, ,
, .长方形
.长方形 由点
由点 与点
与点 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿 轴正方向作匀速直线运动,当点
轴正方向作匀速直线运动,当点 与点
与点 重合时停止运动.设长方形运动的时间为
重合时停止运动.设长方形运动的时间为 秒,长方形
秒,长方形 与△
与△ 重合部分的面积为
重合部分的面积为 .
.

(1)求直线 的解析式;
的解析式;
(2)当 =1时,请判断点
=1时,请判断点 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
(3)请求出当 为何值时,点
为何值时,点 在直线
在直线 上;
上;
(4)直接写出在整个运动过程中 与
与 的函数关系式.
的函数关系式.
【答案】
(1) ;(2)在;(3)
;(2)在;(3) =3;
=3;
(4)  .
.
【解析】
试题分析:(1)把点 (4,0)代入直线
(4,0)代入直线 即可求得结果;
即可求得结果;
(2)先求出当 =1时点A运动的路程,即可得到点C的坐标,再代入直线MN的解析式即可判断;
=1时点A运动的路程,即可得到点C的坐标,再代入直线MN的解析式即可判断;
(3)先得到运动开始时点D坐标,再令 ,得到此时点D的坐标即可判断;
,得到此时点D的坐标即可判断;
(4)分 、
、 、
、 、
、 四种情况分析即可.
四种情况分析即可.
(1)∵直线 与
与 轴交于点
轴交于点 (4,0)
(4,0)
∴ ,解得
,解得
∴直线 的解析式为
的解析式为 ;
;
(2)如图1,当 =1时,点
=1时,点 在直线
在直线 上,
上,

当 =1时,点A运动的路程为AO=1×1=1,
=1时,点A运动的路程为AO=1×1=1,
又∵ ,
,
∴此时点C的坐标为(3,1)
把点C的坐标代入直线MN的解析式
∵
∴点 在直线
在直线 上;
上;
(3)如图2,点 向右平移过程中纵坐标不变
向右平移过程中纵坐标不变

由题意知,运动开始时点D坐标为(0,1)
令 ,解得
,解得
此时点D的坐标为(3,1)
∴ ;
;
即 =3时,点
=3时,点 在直线
在直线 上;
上;
(4) .
.
考点:本题考查的是一次函数的应用
点评:解答本题的关键是熟练掌握待定系数法求函数关系式,函数图象上的点的坐标适合函数关系式,即代入函数关系式后,函数关系式的左右两边相等.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图,直线l与双曲线交于A、B两点,C是线段BA延长线上的点,D是双曲线上一点(D都不与A、B重合),点C、D都在第一象限,过点C、D分别向x轴作垂线,垂足分别为E、F,连接OC、OD,设△COE的面积为S1,△DOF的面积为S2,则S1、S2的大小关系为
如图,直线l与双曲线交于A、B两点,C是线段BA延长线上的点,D是双曲线上一点(D都不与A、B重合),点C、D都在第一象限,过点C、D分别向x轴作垂线,垂足分别为E、F,连接OC、OD,设△COE的面积为S1,△DOF的面积为S2,则S1、S2的大小关系为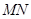 :
: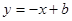 与
与 轴交于点
轴交于点 (4,0),与
(4,0),与 轴交于点
轴交于点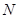 ,长方形
,长方形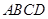 的边
的边 在
在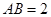 ,
,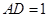 .长方形
.长方形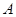 与点
与点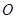 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿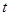 秒,长方形
秒,长方形 重合部分的面积为
重合部分的面积为 .
.
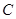 是否在直线
是否在直线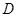 在直线
在直线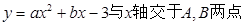 ,与
,与 轴交于点
轴交于点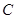 ,且
,且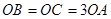 .
.
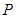 ,使得以点
,使得以点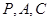 为顶点的三角形为直角三角形?
为顶点的三角形为直角三角形?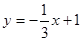 交
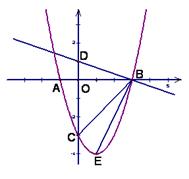
交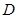 点,
点,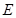 为抛物线顶点.若
为抛物线顶点.若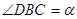 ,
, 的值.
的值. 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若

 上有一动点P,当
上有一动点P,当 时,求出点
时,求出点 的坐标;
的坐标; ,
, 是线段
是线段 、
、 重合)的一个动点.过点
重合)的一个动点.过点 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 .当t为何值时,
.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?