题目内容
如图1,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若

1.求抛物线的解析式
2.抛物线对称轴 上有一动点P,当
上有一动点P,当 时,求出点
时,求出点 的坐标;
的坐标;
3.如图2所示,连结 ,
, 是线段
是线段 上(不与
上(不与 、
、 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的横坐标为
的横坐标为 .当t为何值时,
.当t为何值时, 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
【答案】
1.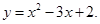
2.点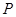 的坐标为(
的坐标为(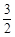 ,
,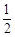 )或(
)或(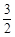 ,
,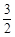 )
)
3.见解析
【解析】解:(1)∵抛物线 过点
过点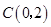 . ∴
. ∴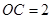
又∵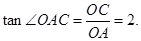 ∴
∴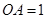 ,即
,即 ………………………1分
………………………1分
又∵点A在抛物线 上.
上.
∴0=12+b×1+2,b=-3
∴抛物线的解析式为: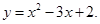 …………………2分
…………………2分
(2)过点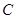 作对称轴
作对称轴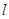 的垂线,垂足为
的垂线,垂足为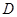 ,
,
∴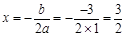 .
.
∴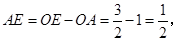 ………………………3分
………………………3分
∵
∴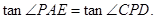
∴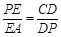 ,即
,即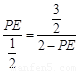 ,………………………..4分
,………………………..4分
解得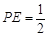 或
或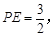 ∴点
∴点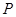 的坐标为(
的坐标为(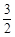 ,
,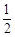 )或(
)或(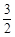 ,
,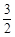 ). ………………5分
). ………………5分
(备注:可以用勾股定理或相似解答)
(3)易得直线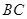 的解析式为
的解析式为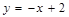 ,
,
∵点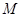 是直线
是直线 和线段
和线段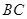 的交点,
的交点,
∴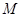 点的坐标为
点的坐标为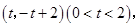
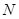 的坐标为
的坐标为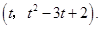 ………………6分
………………6分
∴ ………………………….7分
………………………….7分
∴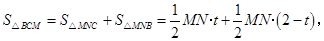
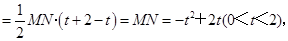 ……..........................8分
……..........................8分
∴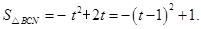
∴当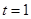 时,
时,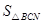 最大值为1. …………………………………………9分
最大值为1. …………………………………………9分
(备注:如果没有考虑的取值范围,可以不扣分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

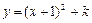 与
与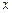 轴交于A、B两点,与
轴交于A、B两点,与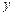 轴交于点C(0,
轴交于点C(0,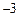 ).
).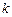 的值;
的值;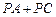 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
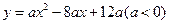 与
与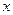 轴交于
轴交于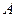 、
、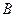 两点(点
两点(点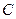 在第一象限,满足∠
在第一象限,满足∠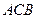 为直角,且恰使△
为直角,且恰使△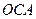 ∽△
∽△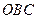 .
.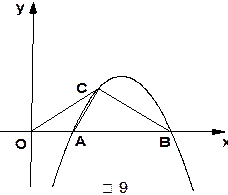
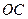 的长.
的长. 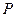 ,使△
,使△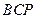 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的 与
与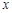 轴交于A、B两点,与
轴交于A、B两点,与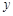 轴交于点C(0,
轴交于点C(0,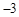 ).
).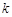 的值;
的值;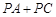 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
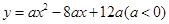 与
与 轴交于
轴交于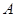 、
、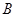 两点(点
两点(点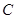 在第一象限,满足∠
在第一象限,满足∠ 为直角,且恰使△
为直角,且恰使△ ∽△
∽△ .
.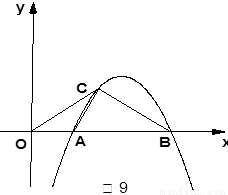
 的长.
的长. 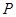 ,使△
,使△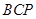 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的