题目内容
 如图,直线l与双曲线交于A、B两点,C是线段BA延长线上的点,D是双曲线上一点(D都不与A、B重合),点C、D都在第一象限,过点C、D分别向x轴作垂线,垂足分别为E、F,连接OC、OD,设△COE的面积为S1,△DOF的面积为S2,则S1、S2的大小关系为
如图,直线l与双曲线交于A、B两点,C是线段BA延长线上的点,D是双曲线上一点(D都不与A、B重合),点C、D都在第一象限,过点C、D分别向x轴作垂线,垂足分别为E、F,连接OC、OD,设△COE的面积为S1,△DOF的面积为S2,则S1、S2的大小关系为S1<S2
S1<S2
.(用“<”连接)分析:先设出反比例函数的解析式,再在双曲线上取一点G,作GH⊥x轴,使GH=CE,连接OG,得出S△GOH=S△DOF,再根据S△GOH>S△COE,得出S△COE<S△DOF,即可得出答案.
解答:解:设反比例函数的解析式为y=
 ,
,
在双曲线上取一点G,作GH⊥x轴,使GH=CE,连接OG,
则S△GOH=S△DOF=
,
∵OH>OE,
∴S△GOH>S△COE,
∴S△COE<S△DOF,
∴S1<S2;
故答案为:S1<S2.
| k |
| x |
 ,
,在双曲线上取一点G,作GH⊥x轴,使GH=CE,连接OG,
则S△GOH=S△DOF=
| k |
| 2 |
∵OH>OE,
∴S△GOH>S△COE,
∴S△COE<S△DOF,
∴S1<S2;
故答案为:S1<S2.
点评:此题考查了反比例函数y=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形的面积为
|k|,是经常考查的一个知识点.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线AB与双曲线的一个交点为点C,CD⊥x轴与点D,OD=2OB=4OA=4. 求一次函数和反比例函数的解析式.
如图,直线AB与双曲线的一个交点为点C,CD⊥x轴与点D,OD=2OB=4OA=4. 求一次函数和反比例函数的解析式.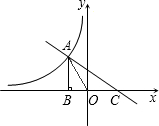 O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.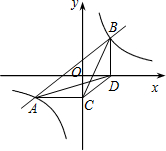 如图,直线AB与双曲线y=
如图,直线AB与双曲线y=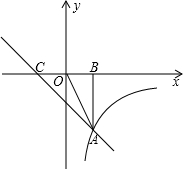 轴于点B,且CO=2BO.
轴于点B,且CO=2BO.