题目内容
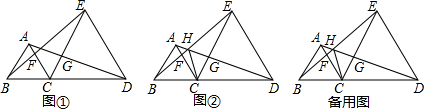
20.已知:如图,在Rt△ABC中AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,满足PB=PD,∠PBO=25°.(1)如图1,求∠DPC的度数;
(2)如图2,过点D作AC的垂线段DE,求证:DE=PO.

分析 (1)如图1中,作PM⊥BC于M交BO于N.由∠BNM=∠CPM=45°,推出∠BPN+∠NBP=∠NPD+∠CPD,由PB=PD,PM⊥BD,推出∠NPB=∠NPD,由此推出∠DPC=∠OBP.
(2)欲证明DE=PO,只要证明△PBO≌△DPE即可.
解答 (1)解:如图1中,作PM⊥BC于M交BO于N.
∵AB=BC,∠ABC=90°,
∴∠C=∠A=45°,∵PM⊥BC,
∴∠PMC=∠NMB=90°,
∴∠C=∠CPM=45°,
∵BO⊥AC,
∴∠CBO=∠ABO=45°,
∴∠MNB=∠MBN=45°,
∴∠BNM=∠CPM,
∴∠BPN+∠NBP=∠NPD+∠CPD,
∵PB=PD,PM⊥BD,
∴∠NPB=∠NPD,
∴∠DPC=∠PBO=25°.
(2)证明:如图2中,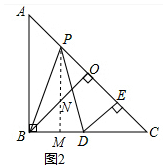
由(1)可知∠DPE=∠PBO,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△PBO和△DPE中,
$\left\{\begin{array}{l}{∠BOP=∠DEP}\\{∠OBP=∠DPE}\\{PB=PD}\end{array}\right.$,
∴△PBO≌△DPE,
∴PO=DE.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
 某花卉市场举行开业庆祝活动,组织者按树木花草的品种和大小,摆成如图所示的图案(每个小圆点代表一盆花),试求第n个图形需要多少盆花?
某花卉市场举行开业庆祝活动,组织者按树木花草的品种和大小,摆成如图所示的图案(每个小圆点代表一盆花),试求第n个图形需要多少盆花?