题目内容
如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A(n,m),且(m-4)2+n2-8n=-16,过C点作∠ECF分别交线段AB、OB于E、F两点.
(1)求A点的坐标;
(2)若OF+BE=AB,求证:CF=CE;
(3)如图(2),若∠ECF=45°,求证:OF+AE=EF.

(1)求A点的坐标;
(2)若OF+BE=AB,求证:CF=CE;
(3)如图(2),若∠ECF=45°,求证:OF+AE=EF.

考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)根据(m-4)2+n2-8n=-16即可求得m、n的值,即可求得A点坐标;
(2)根据勾股定理可以分别求得CF,CE的长,即可解题;
(3)将△ACE顺时针旋转90°,则FG=AE+OF,CG=CE,即可证明△GCF≌△ECF,可得FG=EF,即可解题.
(2)根据勾股定理可以分别求得CF,CE的长,即可解题;
(3)将△ACE顺时针旋转90°,则FG=AE+OF,CG=CE,即可证明△GCF≌△ECF,可得FG=EF,即可解题.
解答:解:(1)点A坐标满足,(m-4)2+n2-8n=-16,
整理得:(m-4)2+(n-4)2=0,
∴m=n=4,
∴点A坐标(4,4);
(2)∵OF+BE=AB,AE+BE=AB,
∴OF=AE,
∵CE=
,CF=
,AC=CO,
∴CF=CE;
(3)将△ACE顺时针旋转90°,则FG=AE+OF,CG=CE,
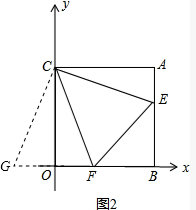
∵∠ECF=45°,
∴∠OCF+∠ACE=45°,∴∠GCF=45°,
在△GCF和△ECF中,
,
∴△GCF≌△ECF(SAS),
∴FG=EF,
∵FG=AE+OF,
∴EF=AE+OF.
整理得:(m-4)2+(n-4)2=0,
∴m=n=4,
∴点A坐标(4,4);
(2)∵OF+BE=AB,AE+BE=AB,
∴OF=AE,
∵CE=
| AC2+AE2 |
| OF2+OC2 |
∴CF=CE;
(3)将△ACE顺时针旋转90°,则FG=AE+OF,CG=CE,

∵∠ECF=45°,
∴∠OCF+∠ACE=45°,∴∠GCF=45°,
在△GCF和△ECF中,
|
∴△GCF≌△ECF(SAS),
∴FG=EF,
∵FG=AE+OF,
∴EF=AE+OF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△GCF≌△ECF是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,∠DOE:∠BOE=1:2,∠DOC:∠COA=1:2,如果∠AOB=120°,那么∠EOC是多少度?
如图,∠DOE:∠BOE=1:2,∠DOC:∠COA=1:2,如果∠AOB=120°,那么∠EOC是多少度?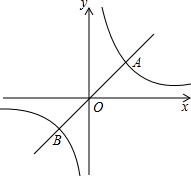 如图,定义:若双曲线y=
如图,定义:若双曲线y= 已知△ABC的内心为O,∠BOC=110°,则∠BAC=
已知△ABC的内心为O,∠BOC=110°,则∠BAC=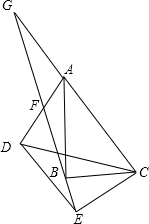 如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点.
如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点. 如图,△ABC中,D是AB的黄金分割点(AD<BD),过点D作DE∥BC交AC于E,若BC=3+
如图,△ABC中,D是AB的黄金分割点(AD<BD),过点D作DE∥BC交AC于E,若BC=3+ 如图,在四边形ABCD中,AB∥CD,∠A=∠C=90°,AC=CD,AB=
如图,在四边形ABCD中,AB∥CD,∠A=∠C=90°,AC=CD,AB=