题目内容
如图，在四边形ABCD中，AB∥CD，∠A=∠C=90°，AC=CD，AB=| 1 |
| 4 |
考点：相似三角形的判定
专题：证明题
分析：由条件可知AE=EC=
CD，则可得到
=
，则可证得结论．
| 1 |
| 2 |
| AB |
| EC |
| AE |
| CD |
解答：证明：
∵AC=CD，E是AC的中点，
∴AE=EC=
CD，
∵AB=
CD，
∴
=
=
，
∵∠A=∠C，
∴△ABE∽△CED．
∵AC=CD，E是AC的中点，
∴AE=EC=
| 1 |
| 2 |
∵AB=
| 1 |
| 4 |
∴
| AB |
| EC |
| AE |
| CD |
| 1 |
| 2 |
∵∠A=∠C，
∴△ABE∽△CED．
点评：本题主要考查相似三角形的判定，利用中点和条件得到
=
是解题的关键．
| AB |
| EC |
| AE |
| CD |
练习册系列答案
相关题目
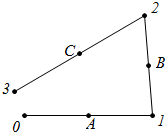如图，平面内有不在同一直线上的三个定点A，B，C，一只青蛙从图中的0号位置出发，跳到关于点A对称的1号位置，再跳到关于点B对称的2号位置，然后又跳到关于点C对称的3号位置，在跳到关于A对称的4号位置，如此继续，一直对称的跳下去，现在要问：第2004号位置与0号位置之间的距离是多少？
已知：在△ABC中，D为BC上一点，EG∥BC，分别交AB、AD、AC于点E、F、G，求证：AE：AF：AG=BE：DF：CG．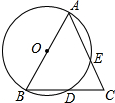
如图，在△ABC中，AB=AC，∠BAC=50°，以AB为直径的圆分别交BC、AC于点D、E，则
