题目内容
7.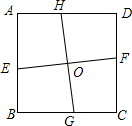 如图,点O是正方形ABCD的中心,E、F、G、H分别是边AB、CD、BC、AD上的点,且EF⊥GH,EF、GH相交于点O,下列结论:①AE=BG;②∠BEO=∠CGO;③OE=OH;④S正方形ABCD≠4S四边形AEOH中正确的有( )
如图,点O是正方形ABCD的中心,E、F、G、H分别是边AB、CD、BC、AD上的点,且EF⊥GH,EF、GH相交于点O,下列结论:①AE=BG;②∠BEO=∠CGO;③OE=OH;④S正方形ABCD≠4S四边形AEOH中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 连接OA、OB、OC、OD,由点O是正方形ABCD的中心,得出∠AOB=90°,∠OAE=∠OBG=45°,OA=OB=OC=OD,由ASA证明△AOE≌△BOG,得出对应边相等AE=BG,得出①正确;
同理:△OBE≌△OCG,得出∠BEO=∠CGO,②正确;
同理:△AOH≌△BOE,得出OE=OH,③正确;
由四边形AEOH的面积=四边形BGOE的面积=$\frac{1}{4}$正方形ABCD的面积,得出正方形ABCD的面积=4四边形AEOH的面积,得出④不正确.
解答 解:连接OA、OB、OC、OD,如图所示:
∵点O是正方形ABCD的中心,
∴∠AOB=90°,∠OAE=∠OBG=45°,OA=OB=OC=OD,
∵EF⊥GH,
∴∠EOG=90°,
∴∠AOE=∠BOG,
在△AOE和△BOG中,$\left\{\begin{array}{l}{∠OAE=∠OBG}&{\;}\\{OA=OB}&{\;}\\{∠AOE=∠BOG}&{\;}\end{array}\right.$,
∴△AOE≌△BOG(ASA),
∴AE=BG,①正确;
同理:△OBE≌△OCG,
∴∠BEO=∠CGO,②正确;
同理:△AOH≌△BOE,
∴OE=OH,③正确;
∴四边形AEOH的面积=四边形BGOE的面积=$\frac{1}{4}$正方形ABCD的面积,
∴正方形ABCD的面积=4四边形AEOH的面积,
∴④不正确;
正确的有3个.故选:C.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,在△ABC中,已知AC=8cm,BC=6cm,AD⊥BC于点D,BE⊥AC于点E,AD=7cm,求BE的长.
如图,在△ABC中,已知AC=8cm,BC=6cm,AD⊥BC于点D,BE⊥AC于点E,AD=7cm,求BE的长.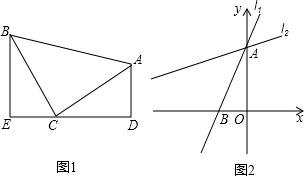
 .
.