题目内容
14.如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x+6与x、y轴分别交于点A、点B,将线段BA绕着B点逆时针方向旋转90°,得到线段BC.(1)求C点的坐标;
(2)连接AC,点D为BC的中点,过D作AC的垂线EF,交AC于E,交直线AB于F,连AD.若点P为射线AD上的一动点,连接PC、PF,当点P在射线AD上运动时,PF2-PC2的值是否发生改变?若改变,请求出其范围;若不变,求出其值并说明理由.
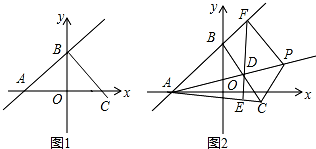
分析 (1)首先求得A、B的坐标和AB的长,过C作CD垂直于y轴,设出C坐标,利用AAS得到三角形AOB与三角形BDC全等,利用全等三角形对应边相等得到两对边相等,求出m与n的值,即可确定出C坐标;
(2)如图2所示,连接CF交AP于点H,利用SAS得到三角形ABD与三角形CBF全等,利用全等三角形对应角相等得到∠BAD=∠BCF,再由对顶角相等得到∠CHD=∠ABD=90°,即CH垂直于AP,利用勾股定理得到PF2-PC2=(FH2+PH2)-(CH2+PH2)=PH2-CH2,再由FH2-CH2=(DF2-DH2)-(DC2-DH2)=DF2-DC2,求出BD与DC的长,进而得到DF的长,确定出PF2-PC2的为25.
解答 解:(1)令y=0得:$\frac{3}{4}x+6=0$,解得:x=-8,
∴OA=8.
令x=0得:y=6,
∴OB=6.
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
如图1所示,过C作CD⊥y轴交于点D,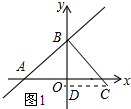
依题意设C(m,n)(m>0,n<0),
∵AB=BC,且AB⊥BC,
∴∠BAO+∠ABO=∠DBC+∠ABO=90°,
∴∠BAO=∠DBC,
在△AOB和△BDC中,$\left\{\begin{array}{l}{∠AOB=∠BDC=90°}\\{∠BAO=∠CBD}\\{AB=BC}\end{array}\right.$,
∴△AOB≌△BDC(AAS),
∴BD=OA,DC=OB,即6-n=8,m=6,
∴n=-2,
则C坐标为(6,-2);
(2)不变.
理由:如图2所示,连接CF交AP于点H.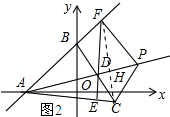
依题意得:△ABC为等腰直角三角形,即∠BAC=∠ACB=45°,
∵EF⊥AC,
∴△AEF为等腰直角三角形.
∴∠BFD=45°.
∴△BDF为等腰直角三角形.
∴BF=BD.
在△ABD和△CBF中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBF=90°}\\{BD=BF}\end{array}\right.$,
∴△ABD≌△CBF(SAS).
∴∠BAD=∠BCF.
∵∠ABD=∠PDC,
∴∠DHC=∠ABC=90°,即CF⊥AP.
∴PF2-PC2=(FH2+PH2)-(CH2+PH2)=PH2-CH2.
∵FH2-CH2=(DF2-DH2)-(DC2-DH2)=DF2-DC2,
∵AB=BC=10,D为BC的中点,
∴BD=DC=5.
∵△BDF为等腰直角三角形,
∴DF=$\sqrt{2}$BD=5$\sqrt{2}$,
∴PF2-PC2=DF2-DC2=25.
点评 本题主要考查的是一次函数综合题,涉及的知识有:全等三角形的判定与性质,勾股定理,坐标与图形性质,等腰直角三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

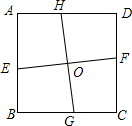 如图,点O是正方形ABCD的中心,E、F、G、H分别是边AB、CD、BC、AD上的点,且EF⊥GH,EF、GH相交于点O,下列结论:①AE=BG;②∠BEO=∠CGO;③OE=OH;④S正方形ABCD≠4S四边形AEOH中正确的有( )
如图,点O是正方形ABCD的中心,E、F、G、H分别是边AB、CD、BC、AD上的点,且EF⊥GH,EF、GH相交于点O,下列结论:①AE=BG;②∠BEO=∠CGO;③OE=OH;④S正方形ABCD≠4S四边形AEOH中正确的有( )