题目内容
2.模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.易证:△BEC≌△CDA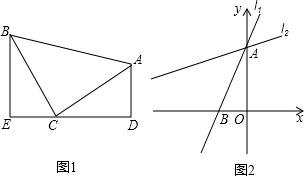
模型应用:如图2,已知直线l1:y=$\frac{4}{3}$x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2.
(1)在直线l2上求点C,使△ABC为直角三角形;
(2)求l2的函数解析式;
(3)在直线l1、l2分别存在点P、Q,使得点A、O、P、Q四点组成的四边形是平行四边形?请直接写出点Q的坐标.
分析 (1)过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,根据∠BAC=45°可知△ABC为等腰Rt△,由(1)可知△CBD≌△BAO,由全等三角形的性质得出C点坐标;
(2)利用待定系数法求出直线l2的函数解析式即可;
(3)设Q1的横坐标为x,则Q1(x,$\frac{1}{7}$x+4),P(x,$\frac{4}{3}$x+4),先求得OA的长,根据平行四边形的性质得出$\frac{1}{7}$x+4-($\frac{4}{3}$x+4)=4,求得x=-$\frac{84}{25}$,从而求得Q1的坐标,根据AQ1=OP=AQ2,求得Q2的横坐标为$\frac{84}{25}$,即可求得Q2($\frac{84}{25}$,$\frac{112}{25}$).
解答 (1)解:过点B作BC⊥AB于点B,交l2于点C,过C作CD⊥x轴于D,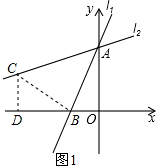 如图1,
如图1,
∵∠BAC=45°,
∴△ABC为等腰Rt△,
∵△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=$\frac{4}{3}$x+4,
∴A(0,4),B(-3,0),
∴BD=AO=4.CD=OB=3,
∴OD=4+3=7,
∴C(-7,3);
(2)设l2的解析式为y=kx+b(k≠0),
∵A(0,4),C(-7,3);
∴$\left\{\begin{array}{l}{b=4}\\{-7k+b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{1}{7}}\\{b=4}\end{array}\right.$,
∴l2的解析式:y=$\frac{1}{7}$x+4;
(3)如图2,①当AO为边时,
∵A(0,4),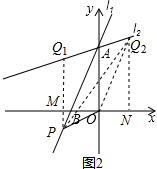
∴OA=4,设Q1的横坐标为x,
则Q1(x,$\frac{1}{7}$x+4),P(x,$\frac{4}{3}$x+4),
∵四边形AOPQ是平行四边形,
∴PQ1=OA=4,
即$\frac{1}{7}$x+4-($\frac{4}{3}$x+4)=4,或$\frac{4}{3}$x+4-($\frac{1}{7}$x+4)=4,
解得x=-$\frac{84}{25}$或$\frac{84}{25}$
∴Q1(-$\frac{84}{25}$,$\frac{88}{25}$)或($\frac{84}{25}$,$\frac{112}{25}$).
②当AO为对角线时,作OQ2∥AB,
直线OQ2解析式为y=$\frac{4}{3}$x,
由$\left\{\begin{array}{l}{y=\frac{4}{3}x}\\{y=\frac{1}{7}x+4}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{84}{25}}\\{y=\frac{112}{25}}\end{array}\right.$,
∴Q2($\frac{84}{25}$,$\frac{112}{25}$).
综上,存在符合条件的平行四边形,且Q点的坐标为(-$\frac{84}{25}$,$\frac{88}{25}$)或($\frac{84}{25}$,$\frac{112}{25}$).
点评 本题考查的是一次函数综合题,涉及到点的坐标、平行四边形的性质、一次函数的应用、等腰直角三角形以及全等三角形等相关知识的综合应用,需要考虑的情况较多,难度较大.

 阅读快车系列答案
阅读快车系列答案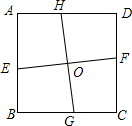 如图,点O是正方形ABCD的中心,E、F、G、H分别是边AB、CD、BC、AD上的点,且EF⊥GH,EF、GH相交于点O,下列结论:①AE=BG;②∠BEO=∠CGO;③OE=OH;④S正方形ABCD≠4S四边形AEOH中正确的有( )
如图,点O是正方形ABCD的中心,E、F、G、H分别是边AB、CD、BC、AD上的点,且EF⊥GH,EF、GH相交于点O,下列结论:①AE=BG;②∠BEO=∠CGO;③OE=OH;④S正方形ABCD≠4S四边形AEOH中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\left\{\begin{array}{l}{x-y>0}\\{y+z>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}-x>0}\\{x+1<0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+2>0}\\{x+y<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+3>0}\\{x>0}\end{array}\right.$ |