题目内容
如图，在菱形ABCD中，AE⊥BC，若cos∠B=| 4 |
| 5 |
考点：菱形的性质
专题：
分析：根据菱形的性质得出AB=BC=CD=AD，根据cosB=
=
设BE=4x，得出AB=BC=5x，求出x，求出AB、BE，根据勾股定理求出AE即可．
| BE |
| AB |
| 4 |
| 5 |
解答：解：∵四边形ABCD是菱形，
∴AB=BC=CD=AD，
∵cosB=
=
，
∴设BE=4x，则AB=BC=5x，
∵EC=4，
∴5x-4x=4，
x=4，
∴AB=20，BE=16，
在Rt△AEB中，由勾股定理得：AE=
=12，
故答案为：12．
∴AB=BC=CD=AD，
∵cosB=
| BE |
| AB |
| 4 |
| 5 |
∴设BE=4x，则AB=BC=5x，
∵EC=4，
∴5x-4x=4，
x=4，
∴AB=20，BE=16，
在Rt△AEB中，由勾股定理得：AE=
| 202-162 |
故答案为：12．
点评：本题考查了菱形的性质，解直角三角形，勾股定理的应用，解此题的关键是求出AB和BE的长，用了方程思想．
练习册系列答案
阅读快车系列答案
相关题目
如图1，在△ABC中，∠C=90°，AD平分∠BAC，CD=5cm，则点D到AB边的距离是
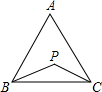如图，在△ABC中，AB=AC，∠A=50°．如果P为三角形内一点，且∠PBC=∠PCA，那么∠BPC等于（ ）| A、100° | B、115° |
| C、130° | D、65° |
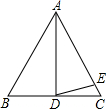如图，在△ABC中，AB=AC，BD=CD，∠BAD=40°，且AD=AE，则∠EDC等于