题目内容
14．
如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E=35°，求∠BAC的度数．
分析 首先由AE∥BD，根据平行线的性质，求得∠DBC的度数，然后由BD平分∠ABC，求得∠ABC的度数，再由AB=AC，利用等边对等角的性质，求得∠C的度数，继而求得答案．
解答 解：∵AE∥BD，
∴∠DBC=∠E=35°，
∵BD平分∠ABC，
∴∠ABC=2∠DBC=70°，
∵AB=AC，
∴∠C=∠ABC=70°，
∴∠BAC=180°-∠ABC-∠C=40°．
点评 此题考查了等腰三角形的性质、平行线的性质以及角平分线的定义．注意等边对等角定理的应用．
练习册系列答案
相关题目
4．
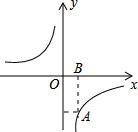如图，函数y=$\frac{k}{x}$的图象经过点A（1，-3），AB垂直x轴于点B，则下列说法正确的是（ ）
如图，函数y=$\frac{k}{x}$的图象经过点A（1，-3），AB垂直x轴于点B，则下列说法正确的是（ ）| A． | k=3 | B． | x＜0时，y随x增大而增大 | ||
| C． | S△AOB=3 | D． | 函数图象关于y轴对称 |
如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以60海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为30$\sqrt{2}$海里．
如图，平行于x轴的直线l与y轴、直线y=3x、直线y=x分别交于点A、B、C．则下列结论正确的个数有（ ）
如图，AC和BD相交于点O，OA=OC，OB=OD．求证：