题目内容
5.某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少?
分析 (1)本题首先找出题中的等量关系即甲种原料不超过360千克,乙种原料不超过290千克,然后列出不等式组并求出它的解集.由此可确定出具体方案.
(2)根据题意列出W与x之间的函数关系式,利用一次函数的增减性和(1)得到的取值范围即可求得最大利润.
解答 解:(1)设安排生产A种产品x件,则生产B种产品(50-x)件,
根据题意有:$\left\{\begin{array}{l}{9x+4(50-x)≤360}\\{3x+10(50-x)≤290}\end{array}\right.$,
解得:30≤x≤32,
∵x为整数,
∴x30,31,32,
所以有三种方案:①安排A种产品30件,B种产品20件;
②安排A种产品31件,B种产品19件;
③安排A种产品32件,B种产品18件.
(2)设安排生产A种产品x件,
那么利润为:W=700x+1200(50-x)=-500x+60000,
∵k=-500<0,
∴W随x的增大而减小,
∴当x=30时,对应方案的利润最大,W=-500×30+60000=45000,最大利润为45000元.
∴采用方案①所获利润最大,为45000元.
点评 本题考查一次函数的应用,一元一次不等式组的应用及最大利润问题;得到两种原料的关系式及总利润的等量关系是解决本题的关键.

练习册系列答案
相关题目
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAD=$\frac{4}{3}$,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAD=$\frac{4}{3}$,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
 某镇枇杷园的枇杷除了运往市区销售外,还可以让市民亲自去园内采摘购买,已知今年3月份该枇杷在市区、园区的销售价格分别为6元/千克、4元/千克,今年3月份一共销售了3000千克,总销售额为16000元.
某镇枇杷园的枇杷除了运往市区销售外,还可以让市民亲自去园内采摘购买,已知今年3月份该枇杷在市区、园区的销售价格分别为6元/千克、4元/千克,今年3月份一共销售了3000千克,总销售额为16000元.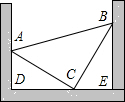 如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积. 如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2-$\sqrt{3}$,FC=2$\sqrt{3}$.
如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2-$\sqrt{3}$,FC=2$\sqrt{3}$. 印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”:
印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”: