Question

4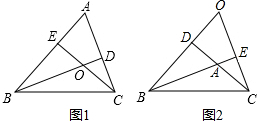．（1）已知如图1，锐角△ABC中，AB、AC边上的高CE、BD相交于O点．若∠A=70°，则∠BOC=110°．
（2）若将（1）题中已知条件“锐角△ABC”改为“钝角△ABC，∠A为钝角且∠A=n°”，其它条件不变（图2），请你求出∠BOC的度数．

Answer 1

分析 （1）根据垂直的定义得到∠ADB=90°，根据三角形内角和定理求出∠ABD，根据三角形的外角的性质解答；
（2）仿照（1）的做法，代入计算即可．

解答 解：（1）∵BD⊥AC，
∴∠ADB=90°，
∴∠ABD+∠A=90°，
∴∠ABD=90°-70°=20°，
∵CE⊥AB，
∴∠BEC=90°，
∴∠BOC=∠BEC+∠ABD=110°，
故答案为：=110°；
（2））∵BD⊥AC，
∴∠ADB=90°，
∴∠ABD+∠A=90°，
∴∠ABD=90°-n°，
∵CE⊥AB，
∴∠BEC=90°，
∴∠BOC=∠BEC+∠ABD=（180-n）°．

点评 本题考查的是三角形内角和定理，掌握三角形内角和等于180°是解题的关键．