题目内容
7.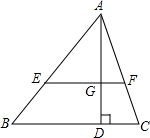 如图,在△ABC中,AD是高,点E在AB上,EF∥BC,分别交AC、AD于点F、G,且 $\frac{EF}{BC}$=$\frac{3}{5}$,求:
如图,在△ABC中,AD是高,点E在AB上,EF∥BC,分别交AC、AD于点F、G,且 $\frac{EF}{BC}$=$\frac{3}{5}$,求:(1)$\frac{AF}{FC}$的值;
(2)$\frac{AG}{AD}$的值.
分析 (1)由EF∥BC可知△AEF∽△ABC,利用相似三角形对应边成比例可求得$\frac{AF}{FC}$的值;
(2)根据相似三角形对应高的比等于对应边的比求解即可.
解答 解:(1)∵EF∥BC,
∴△AEF∽△ABC.
∴$\frac{AF}{AC}=\frac{EF}{BC}=\frac{3}{5}$.
∴$\frac{AF}{FC}=\frac{3}{2}$.
(2)∵△AEF∽△ABC,
∴$\frac{AG}{AD}=\frac{EF}{BC}=\frac{3}{5}$.
点评 本题主要考查的是相似三角形的性质和判定,掌握相似三角形的性质是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
18.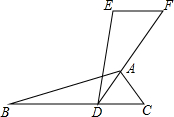 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )| A. | 50° | B. | 60° | C. | 100° | D. | 120° |
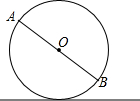 如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.
如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.