题目内容
17.利用等式的性质,在横线上填上适当的数或式子,并在括号内写明变形的根据(1)如果2x-3=5,则2x=8,(等式的基本性质1)
x=4;(等式的基本性质2)
(2)如果5x=2x-4,则3x=-4,(等式的基本性质1)
x=-$\frac{4}{3}$;(等式的基本性质2)
(3)如果$\frac{1}{3}$x=2x-3,则-$\frac{5}{3}$x=-3,(等式的基本性质1)
x=-$\frac{5}{3}$;(等式的基本性质2)
分析 (1)先根据等式的基本性质1得出2x=8,再由等式的基本性质2即可得出结论;
(2)先根据等式的基本性质1得出3x=-4,再由等式的基本性质2即可得出结论;
(3)先根据等式的基本性质1得出-$\frac{5}{3}$x=-3,再由等式的基本性质2即可得出结论.
解答 解:(1)方程两边同时加3得,2x=8,
方程两边同时除以2得,x=4.
故答案为:8,等式的基本性质1;4,等式的基本性质2;
(2)方程两边同时减去2x得,3x=-4,
方程两边同时除以3得,x=-$\frac{4}{3}$.
故答案为:-4,等式的基本性质1;-$\frac{4}{3}$,等式的基本性质2;
(3)方程两边同时减去2x得,-$\frac{5}{3}$x=-3,
方程两边同时除以-$\frac{5}{3}$得,x=-$\frac{9}{5}$
故答案为:-3,等式的基本性质1;-$\frac{5}{3}$,等式的基本性质2.
点评 本题考查的是的等式的基本性质,熟记等式的2个基本性质是解答此题的关键.

练习册系列答案
相关题目
6.已知一次函数y=ax+b(a≠0),x,y的部分对应值如下表.那么关于x的方程ax+b=0的解是x=2
| x | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
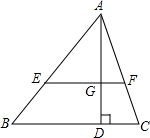 如图,在△ABC中,AD是高,点E在AB上,EF∥BC,分别交AC、AD于点F、G,且 $\frac{EF}{BC}$=$\frac{3}{5}$,求:
如图,在△ABC中,AD是高,点E在AB上,EF∥BC,分别交AC、AD于点F、G,且 $\frac{EF}{BC}$=$\frac{3}{5}$,求: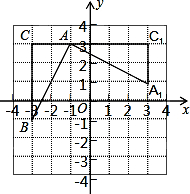 如图,平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
如图,平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.