题目内容
10. 如图,△ABC中,AB=AC=8,BC=12,点P、Q分别在AB、BC边上,且∠AQP=∠B.
如图,△ABC中,AB=AC=8,BC=12,点P、Q分别在AB、BC边上,且∠AQP=∠B.(1)求证:△BQP∽△CAQ;
(2)若BP=4.5,求∠BPQ的度数;
(3)若在BC边上存在两个点Q,满足∠AQP=∠B,求BP长的取值范围.
分析 (1)根据等腰三角形的性质得到∠B=∠C,根据三角形的外角的性质得到∠PQB=∠CAQ,根据相似三角形的判定定理证明结论;
(2)根据相似三角形的性质求出BQ=6,根据等腰三角形的三线合一得到∠CQA=90°,根据相似三角形的性质得到答案;
(3)设BQ=x,BP=m,根据相似三角形的性质得到一元二次方程,根据题意和根的判别式计算即可.
解答 解:(1)∵AB=AC,
∴∠B=∠C.
∵∠AQP=∠B.
∴∠AQP=∠C.
又∵∠AQB=∠AQP+∠PQB,∠AQB=∠CAQ+∠C,
∴∠PQB=∠CAQ.
∴△BQP∽△CAQ.
(2)∵△BQP∽△CAQ,
∴$\frac{BQ}{AC}$=$\frac{BP}{CQ}$.
∴$\frac{BQ}{8}$=$\frac{4.5}{12-BQ}$,
解得BQ=6.
∵BC=12,
∴BQ=CQ=6.
又∵AB=AC,
∴AQ⊥BC,
∴∠CQA=90°.
∵△BQP∽△CAQ,
∴∠BPQ=∠CQA=90°.
(3)∵△BQP∽△CAQ,
∴$\frac{BQ}{AC}$=$\frac{BP}{CQ}$.
设BQ=x,BP=m,则 $\frac{x}{8}$=$\frac{m}{12-x}$,
整理得 x2-12x+8m=0.
∵在BC边上存在两个点Q,
∴方程有两个不相等的正实数根,
∴△=122-32m>0,解得 m<$\frac{9}{2}$,
∴BP长的取值范围为0<BP<$\frac{9}{2}$.
点评 本题考查的是相似三角形的判定和性质以及一元二次方程根的判别式的应用,掌握相似三角形的对应边的比相等是解题的关键.

练习册系列答案
相关题目
15. 如图,正方形ABCD的面积是( )
如图,正方形ABCD的面积是( )
 如图,正方形ABCD的面积是( )
如图,正方形ABCD的面积是( )| A. | 5 | B. | 25 | C. | 7 | D. | 10 |
 如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,$\sqrt{3}$≈1.732)
如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,$\sqrt{3}$≈1.732) 如图,△ABC的顶点均在格点上,利用网格线在图中找一点O,使得OA=OB=OC.
如图,△ABC的顶点均在格点上,利用网格线在图中找一点O,使得OA=OB=OC.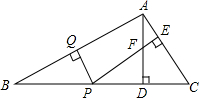 如图,△ABC中.∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC.
如图,△ABC中.∠B=22.5°,AB的垂直平分线交AB于点Q,交BC于点P,PE⊥AC于点E,AD⊥BC于点D,AD交PE于点F.求证:DF=DC. 如图,△CAB,△CDE都是等腰直角三角形,M是DB中点,求证:CM⊥AE.
如图,△CAB,△CDE都是等腰直角三角形,M是DB中点,求证:CM⊥AE.