��Ŀ����
��ͼ1����������ȫ��ͬ��������ֽƬ ��
�� �غϷ��ã�����
�غϷ��ã�����
 .
.
 | |||
 | |||
��1����������
��ͼ2���̶� ��ʹ
��ʹ �Ƶ�
�Ƶ� ˳ʱ����ת������
˳ʱ����ת������ ǡ������
ǡ������ ����ʱ����գ�
����ʱ����գ�
ͼ1 ͼ2
�� �߶� ��
�� ��λ�ù�ϵ�� ��
��λ�ù�ϵ�� ��
�� �� �����Ϊ
�����Ϊ ��
�� �����Ϊ
�����Ϊ ����
���� ��
�� ��������ϵ�� ��֤����Ľ��ۣ�
��������ϵ�� ��֤����Ľ��ۣ�
��2��������֤
 ��
�� �Ƶ�
�Ƶ� ��ת��ͼ3��ʾ��λ��ʱ��С�����루1����
��ת��ͼ3��ʾ��λ��ʱ��С�����루1���� ��
�� ��������ϵ��Ȼ�����������Էֱ�������
��������ϵ��Ȼ�����������Էֱ������� ��
�� ��BC��CE���ϵĸߣ�����֤��С���IJ��룮
��BC��CE���ϵĸߣ�����֤��С���IJ��룮
�⣺��1�����߶� ��
�� ��λ�ù�ϵ�� ƽ�� ��
��λ�ù�ϵ�� ƽ�� ��
��S1��S2��������ϵ�� ��� ��
֤������ͼ2����D��DN��AC��AC�ڵ�N����E��EM��AC��AC�ӳ�����M����C��CF��AB��AB�ڵ�F��
�ɢٿ�֪ ��ADC�ǵȱ������Σ� ��
�� ��
��
 ��DN=CF, DN=EM��
��DN=CF, DN=EM��
��CF=EM��
�� ��
��
�� ��
��
�֡� ,
,
�� �� ͼ2
�� ͼ2
�� ��
�� ��
��
�� =
= ��
��
 ��2��֤������ͼ3����DG��BC�ڵ�G��AH��CE��EC�ӳ����ڵ�H.
��2��֤������ͼ3����DG��BC�ڵ�G��AH��CE��EC�ӳ����ڵ�H.
�� ��
��
�֡� ��
��
�֡� ,
,
���AHC�ա�DGC��
��AH=DG��
�֡�CE=CB, ͼ3
�� ��
��

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д� �ǡ�O��ֱ��,��
�ǡ�O��ֱ��,�� ,����ΪE,���
,����ΪE,��� ,
,

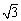 cmΪ�뾶��Բ���
cmΪ�뾶��Բ���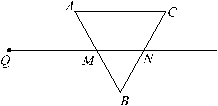

 ��ͼ����ͼ��ʾ������������ԭ��O��ת
��ͼ����ͼ��ʾ������������ԭ��O��ת ������ת��������ߵĽ���ʽΪ( )
������ת��������ߵĽ���ʽΪ( )  B��
B��
 D��
D��

 ��ͼ���ϣ���m��ֵΪ ��ƽ�ƴ˶��κ�����ͼ��ʹ��P������ԭ���غϣ���ƽ�ƺ�ĺ���ͼ������Ӧ�Ľ���ʽΪ .
��ͼ���ϣ���m��ֵΪ ��ƽ�ƴ˶��κ�����ͼ��ʹ��P������ԭ���غϣ���ƽ�ƺ�ĺ���ͼ������Ӧ�Ľ���ʽΪ . ���ڡ�O�ϣ���
���ڡ�O�ϣ��� ����
���� Ϊ
Ϊ B��
B�� C��
C�� D��
D��

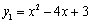 ��ͼ��ΪC1�����κ���
��ͼ��ΪC1�����κ���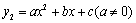 ��ͼ����C1����y��Գƣ�
��ͼ����C1����y��Գƣ�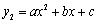 �Ľ���ʽ��
�Ľ���ʽ�� 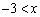 ��0ʱ��ֱ��д��
��0ʱ��ֱ��д��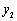 ��ȡֵ��Χ��
��ȡֵ��Χ��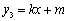 ( k��mΪ������k��0)��ͼ��A��B���㣬��
( k��mΪ������k��0)��ͼ��A��B���㣬�� ʱ��ֱ��д��x��ȡֵ��Χ��
ʱ��ֱ��д��x��ȡֵ��Χ��