题目内容
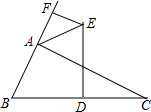 已知:△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=2,AB=3,那么AC长是
已知:△ABC,DE垂直平分BC边,∠BAC外角平分线与DE交于E,过E作EF垂直直线AB于F.若AF=2,AB=3,那么AC长是考点:线段垂直平分线的性质
专题:
分析:过E作EN⊥AC于N,并连接EB、EC,可证得△FAE≌△NAE,进一步可证得△EFB≌△ENC,可得到AC=2AF+AB,可求得AC的长.
解答: 解:过E作EN⊥AC于N,并连接EB、EC.
解:过E作EN⊥AC于N,并连接EB、EC.
∵EA平分∠FAC,
∴∠EAF=∠EAN,
∵EF⊥AB,EN⊥AC,
∴∠EFA=∠ENA=90°,
在△FAE和△NAE中,
,
∴△FAE≌△NAE(AAS),
∴EF=EN,AF=AN,
∵DE垂直平分BC,
∴EB=EC,
在Rt△EFB和Rt△ENC中,
,
∴Rt△EFB≌Rt△ENC(HL),
∴FB=NC,
∴AC=AN+NC=AF+BF=2AF+AB=4+3=7,
故答案为:7.
 解:过E作EN⊥AC于N,并连接EB、EC.
解:过E作EN⊥AC于N,并连接EB、EC.∵EA平分∠FAC,
∴∠EAF=∠EAN,
∵EF⊥AB,EN⊥AC,
∴∠EFA=∠ENA=90°,
在△FAE和△NAE中,
|
∴△FAE≌△NAE(AAS),
∴EF=EN,AF=AN,
∵DE垂直平分BC,
∴EB=EC,
在Rt△EFB和Rt△ENC中,
|
∴Rt△EFB≌Rt△ENC(HL),
∴FB=NC,
∴AC=AN+NC=AF+BF=2AF+AB=4+3=7,
故答案为:7.
点评:本题主要考查线段垂直平分线的性质和全等三角形的判定和性质,通过证明三角形全等得出AC=2AF+AB是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知平行四边形ABCD,下列判断正确的是( )
| A、若∠A=90°,则四边形ABCD是矩形 |
| B、AC=BD |
| C、AB=CD,则ABCD是菱形 |
| D、若AC丄BD,则四边形ABCD为正方形 |
 如图,在⊙O中,AC、BD为直径.求证:AB∥CD.
如图,在⊙O中,AC、BD为直径.求证:AB∥CD.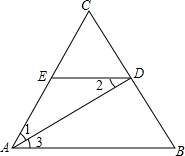 已知,如图,AD平分∠CAB,DE∥AB,求证:∠1=∠2.
已知,如图,AD平分∠CAB,DE∥AB,求证:∠1=∠2. 在△ABC中,点D在直线AB上,在直线BC上取一点E,连接AE,DE,使得 AE=DE,DE交AC于点G,过点D作DF∥AC,交直线BC于点F,∠EAC=∠DEF.
在△ABC中,点D在直线AB上,在直线BC上取一点E,连接AE,DE,使得 AE=DE,DE交AC于点G,过点D作DF∥AC,交直线BC于点F,∠EAC=∠DEF.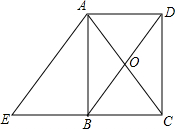 如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AE∥BD,交CB的延长线于点E.
如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AE∥BD,交CB的延长线于点E.