题目内容
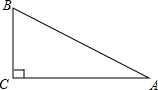
如图,延长直角△ABC的斜边AB到点D,使BD=AB,连接CD,若cot∠BCD=3,则tan∠A的值是( )

| A.1 | B.
| C.9 | D.
|

如图:做DE⊥AC于E,那么BC∥DE,△ABC∽△ADE.
∴
=
,
即
=
.
又由AB=BD,因此AC=CE.
根据BC⊥AC,∠BCE=90°,tan∠DCE=cot(90°-∠EDC)=cot∠BCD=3,
直角三角形DCE中,tan∠DCE=
=3.
直角三角形ADE中,tan∠A=
=
=
.
故选D.

∴
| AB |
| AD |
| AC |
| AE |
即
| AB |
| AB+BD |
| AC |
| AC+CE |
又由AB=BD,因此AC=CE.
根据BC⊥AC,∠BCE=90°,tan∠DCE=cot(90°-∠EDC)=cot∠BCD=3,
直角三角形DCE中,tan∠DCE=
| DE |
| CE |
直角三角形ADE中,tan∠A=
| DE |
| AE |
| DE |
| 2CE |
| 3 |
| 2 |
故选D.


练习册系列答案
相关题目





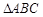 中,
中,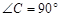 ,
,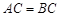 ,若点
,若点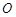 是
是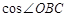 =_______
=_______