题目内容
(本题满分9分)如图,在Rt△ABC中,∠ACB=90,AC=3cm,BC=4cm.动点P从点B出发,以每秒1cm的速度沿射线BA运动,求出点P运动所有的时间t,使得△PBC为等腰三角形.

符合要求的t的值有3个,分别是 ,4,(秒).
【解析】
试题分析:根据等腰三角形的性质,此题要分类讨论三边中腰的情况,所以应有3种可能,然后利用两腰相等即可得出答案.
试题解析:
在Rt△ABC中,∠ACB=90,AC=3cm,BC=4cm.
∴AB=5 cm.
由运动可知,BP=t,且△PBC为等腰三角形有三种可能:
若BP=PC,则∠B=∠PCB.
∵∠ACB=90°,
∴∠PAC=∠PCA,
∴PC=PA,
∴t=BP=AB=.
若BP=BC,则t=4.
若BC=PC,过点C作CH⊥AB,则BP=2BH.由CH×AB=BC×AC,得CH=.
在Rt△BHC中,由勾股定理得BH=.
∴t=BP=.
综上所述,符合要求的t的值有3个,分别是 ,4,(秒).
考点:等腰三角形的性质与判定.

练习册系列答案
相关题目
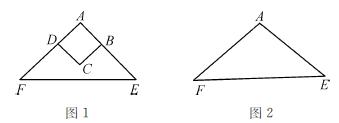


 ,使它与△ABC关于直线l对称.
,使它与△ABC关于直线l对称.
 图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看塑像头顶D的仰角为45°,看塑像底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看塑像头顶D的仰角为45°,看塑像底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: =
= 1.7)
1.7)
