题目内容
如图,在△ABC中,AB=BC,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .

10.
【解析】
试题分析:如图:作三角形ABC关于AC的对称三角形ADC,
连接DE,与AC交于点P,根据两点之间,线段最短得到ED就是PB+PE的最小值,
∵由题知:等腰直角三角形ABC中,∠BAC=45°,
∴∠DAC=45°,
∴∠DAE=90°,
∵B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,
∴AE=6,AD=AB=8,
∴DE= =10,
=10,
故PB+PE的最小值是10.
故答案为:10.

考点:路线最短-对称.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
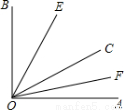
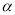 ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);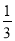 ∠COB,∠COF=
∠COB,∠COF=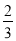 ∠COA”,且∠AOB=
∠COA”,且∠AOB= ; (2)
; (2)  .
.


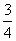 B.
B.  C.
C. 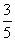 D.
D. 

