题目内容
13.为落实素质教育要求,促进学生全面发展,我市某中学2014年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2016年投资18.59万元.(1)求该学校为新增电脑投资的年平均增长率;
(2)从2014年到2016年,该中学三年为新增电脑共投资多少万元?
分析 (1)设该学校为新增电脑投资的年平均增长率为x,根据以后每年以相同的增长率进行投资,2016年投资18.59万元,列出方程,求出方程的解即可.
(2)根据(1)求出的增长率,就可求出2015年的投资金额,再把2014年,2015年和2016年三年的投资相加,即可得出答案.
解答 解:(1)设该学校为新增电脑投资的年平均增长率为x,根据题意得:
11(1+x)2=18.59,
解得:x1=0.3=30%,x2=-2.3(不合题意,舍去).
答:该学校为新增电脑投资的年平均增长率为30%;
(2)∵2014年投资11万元,
∴2015年投资:11×(1+30%)=14.3万元.
∴该中学三年为新增电脑共投资:11+14.3+18.59=43.89万元.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,注意把不合题意的解舍去.

练习册系列答案
相关题目
3.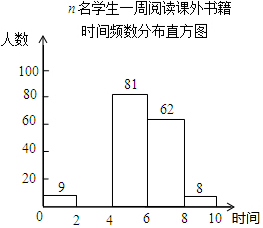 某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.
某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.
n名学生一周阅读课外书籍时间频数分布表
(1)求n的值,并补全频数分布直方图;
(2)这组数据的中位数落在频数分布表中的哪个时间段?
(3)根据上述调查结果,估计该校2400名学生中一周阅读课外书籍时间在6小时以上的人数.
 某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.
某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.n名学生一周阅读课外书籍时间频数分布表
| 时间段 | 频数 |
| 0<t≤2 | 9 |
| 2<t≤4 | 40 |
| 4<t≤6 | 81 |
| 6<t≤8 | 62 |
| 8<t≤10 | 8 |
(2)这组数据的中位数落在频数分布表中的哪个时间段?
(3)根据上述调查结果,估计该校2400名学生中一周阅读课外书籍时间在6小时以上的人数.

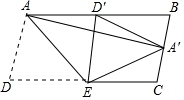 如图,将平行四边形纸片ABCD折叠,使得点D落在AB边上的D'处,折痕为AE.再将△AD'E翻折,点A恰好落在BC的中点A'处,连结AA',若AD=2,则线段AA'的长为$\sqrt{15}$.
如图,将平行四边形纸片ABCD折叠,使得点D落在AB边上的D'处,折痕为AE.再将△AD'E翻折,点A恰好落在BC的中点A'处,连结AA',若AD=2,则线段AA'的长为$\sqrt{15}$.