题目内容
8. 已知:AB是⊙O的直径,C是AB上一点,PC⊥AB,交⊙O于F,PDE是割线,交⊙O于D、E.求证:PC2=PD•PE+AC•CB.
已知:AB是⊙O的直径,C是AB上一点,PC⊥AB,交⊙O于F,PDE是割线,交⊙O于D、E.求证:PC2=PD•PE+AC•CB.
分析 延长PC交⊙O于G,根据切割线定理和相交弦定理进行证明即可.
解答  证明:延长PC交⊙O于G,
证明:延长PC交⊙O于G,
由割线定理,得PD•PE=PF•PG.
由相交弦定理,得AB•BC=CF•CG.
∵直径AB⊥FG,
∴CF=CG,
∴AB•BC=CF2,
∴PD•PE=PF•PG=(PC-CF)(PC+CG)=(PC-CF)(PC+DF)=PC2-CF2,
∴PD•PE+AC•CB=PC2-CF2+CF2=PC2,
即 PC2=PD•PE+AC•CB.
点评 本题考查了切割线定理和相交弦定理.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
20.某校足球比篮球数的2倍多3个,足球数与篮球数的比为3:2,求两种球各有多少.若设足球有x个,篮球有y个,由题意得( )
| A. | $\left\{\begin{array}{l}{x=2y-1}\\{2y=3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2y+3}\\{3x=2y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2y-3}\\{3x=2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2y+3}\\{2x=3y}\end{array}\right.$ |
17.下列条件中,能判定四边形ABCD是矩形的是( )
| A. | 四边形ABCD中,AC=BD | |
| B. | 四边形ABCD中,AC⊥BD | |
| C. | 四边形ABCD中,∠A=90°,∠C=90°,∠D=90° | |
| D. | 四边形ABCD中,∠ABC=90° |
18.把多项式3a2-9ab分解因式,正确的是( )
| A. | 3(a2-3ab) | B. | 3a(a-3b) | C. | a(3a-9b) | D. | a(9b-3a) |
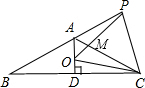 如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )
如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( ) 某中学为了了解七年级600名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
某中学为了了解七年级600名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: