题目内容
11.设y1=1-$\frac{x-1}{2}$,y2=$\frac{x}{3}$(1)当x为何值时,y1,、y2互为相反数;
(2)当x为何值时,y1、y2相等.
分析 (1)利用互为相反数两数之和为0列出方程,求出方程的解即可得到x的值;
(2)根据两式相等列出方程,求出方程的解即可得到x的值.
解答 解:(1)根据题意得:1-$\frac{x-1}{2}$+$\frac{x}{3}$=0,
去分母得:6-3(x-1)+2x=0,
去括号得:6-3x+3+2x=0,
移项合并得:x=9;
(2)根据题意得:1-$\frac{x-1}{2}$=$\frac{x}{3}$,
去分母得:6-3x+3=2x,
移项合并得:5x=9,
解得:x=1.8.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列说法中正确的是( )
| A. | 0不是单项式 | B. | $\frac{1}{x}$是单项式 | C. | πx2y的次数是4 | D. | x-$\frac{3}{2}$是整式 |
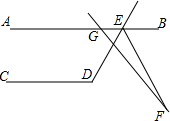 如图,AB∥CD,∠CDE=120°,GF交∠DEB的平分线EF于点F,∠AGF=130°,求∠F的度数.
如图,AB∥CD,∠CDE=120°,GF交∠DEB的平分线EF于点F,∠AGF=130°,求∠F的度数. 如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm.
如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是$\sqrt{289}$cm. 如图,以AB为直径的⊙O与弦CD相交于点E,若AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,求弧BD的长度.(保留π)
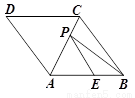
如图,以AB为直径的⊙O与弦CD相交于点E,若AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,求弧BD的长度.(保留π)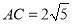 ,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为______.
,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为______.