题目内容
13.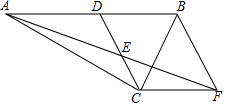 已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB交AE的延长线于点F.
已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB交AE的延长线于点F.(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
分析 (1)先根据点E是CD的中点得出DE=CE,再由AB∥CF可知∠BAF=∠AFC,根据AAS定理可得出△ADE≌△FCE;
(2)根据直角三角形的性质可得出AD=CD=$\frac{1}{2}$AB,再由AB∥CF可知∠BDC=180°-∠DCF=180°-120°=60°,由三角形外角的性质可得出∠DAC=∠ACD=$\frac{1}{2}$∠BDC=30°,进而可得出结论.
解答 (1)证明:∵点E是CD的中点,
∴DE=CE.
∵AB∥CF,
∴∠BAF=∠AFC.
在△ADE与△FCE中,
∵$\left\{\begin{array}{l}{∠BAF=∠AFC}\\{∠AED=∠FEC}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△FCE(AAS);
(2)解:由(1)得,CD=2DE,
∵DE=2,
∴CD=4.
∵点D为AB的中点,∠ACB=90°,
∴AB=2CD=8,AD=CD=$\frac{1}{2}$AB.
∵AB∥CF,
∴∠BDC=180°-∠DCF=180°-120°=60°,
∴∠DAC=∠ACD=$\frac{1}{2}$∠BDC=$\frac{1}{2}$×60°=30°,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4.
点评 本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
3.(-3)-2等于( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
4. 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )| A. | BM=$\frac{1}{2}$AB | B. | AM+BM=AB | C. | AM=BM | D. | AB=2AM |
1.不等式组$\left\{\begin{array}{l}{x-1<2}\\{2x≥4}\end{array}\right.$的解集为( )
| A. | x<3 | B. | x≥2 | C. | 2≤x<3 | D. | 2<x<3 |
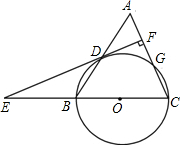 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=44°,∠D=120°,则∠2的度数为38°.
如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=44°,∠D=120°,则∠2的度数为38°.