题目内容
5.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就能拼成一个既不留空隙,又不相互重叠的平面图形,我们称之为镶嵌.一块地板由三种正多边形的小木板镶嵌而成,这三种正多边形的边数分别为a,b,c,求证:$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=$\frac{1}{2}$.分析 多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解答 证明:因为一块地板由三种正多边形的小木板镶嵌而成,这三种正多边形的边数分别为a,b,c,
可得:$180°-\frac{360°}{a}+180°-\frac{360°}{b}+180°-\frac{360°}{c}=360°$,
180°=$\frac{360°}{a}+\frac{360°}{b}+\frac{360°}{c}$,
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{2}$.
点评 本题考查了镶嵌,关键是根据多边形位于同一顶点处的几个角之和能为360°即可.

练习册系列答案
相关题目
 如图所示,△ABC中,AB=AC,∠B=50°,D为BC边的中点,连接AD,那么∠DAC的度数等于40°.
如图所示,△ABC中,AB=AC,∠B=50°,D为BC边的中点,连接AD,那么∠DAC的度数等于40°.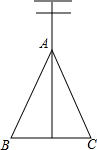 如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.
如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.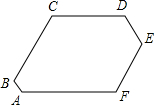 如图,已知六边形ABCDEF的每个内角都是120°且AB=1,DE=2,BC=CD=8,求此六边形的周长.
如图,已知六边形ABCDEF的每个内角都是120°且AB=1,DE=2,BC=CD=8,求此六边形的周长.