题目内容
18.某市为治理污水,需要铺设一段全长为300m的污水排放管道,铺设120m后,为了尽量减少施工对城市交通所造成的影响,每天的工效比原计划增加20%,结果共用30天完成这一任务.(1)求原计划每天铺设管道的长度.
(2)若市政部门原来每天支付工人工资为600元,提高工效后每天支付给工人的工资增长了30%,完成整个工程市政部门应该支付工人工资多少?
分析 (1)设原计划每天铺设管道的长度为xm,则增加后每天的工作效率为(1+20%)x,找出等量关系:铺设120m的时间+铺设(300-120)m的时间=30天,列方程求解即可;
(2)分别得到两种不同的工作效率所用的时间,进一步得到各自需要的工资,相加即可求解.
解答 解:(1)设原计划每天铺设xm管道,则后来的工作效率为(1+20%)x,
根据题意,得$\frac{120}{x}$+$\frac{300-120}{(1+20%)x}$=30,
解得:x=9,
经检验:x=9是原分式方程的解.
答:原计划每天铺设管道的长度为9m.
(2)(1+20%)x=1.2×9=10.8,
120÷9×600+(300-120)÷10.8×600×(1+30%)
=8000+13000
=21000(元).
答:完成整个工程市政部门应该支付工人工资21000元.
点评 本题考查了分式方程的应用,此题涉及的公式:工作时间=工作量÷工作效率,解答本题的关键是读懂题意,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
9. 如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )
如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )
 如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )
如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的周长为( )| A. | 16 | B. | 20 | C. | 12 | D. | 24 |
3.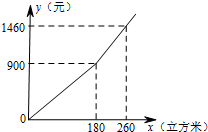 为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
 为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )| A. | 240立方米 | B. | 236立方米 | C. | 220立方米 | D. | 200立方米 |
7.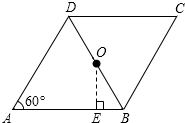 如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )
 如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
 如图,正方形ABCD的边长为a,面积为6;正方形CEFG的边长为b,面积为2.求△BDF的面积.
如图,正方形ABCD的边长为a,面积为6;正方形CEFG的边长为b,面积为2.求△BDF的面积. 如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD.若∠EAO=15°,求∠BOE的度数.
如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD.若∠EAO=15°,求∠BOE的度数.