题目内容
7.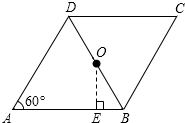 如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
分析 由在菱形ABCD中,∠A=60°,可证得△ABD是等边三角形,又由O为对角线BD的中点,OE⊥AB,可求得OB的长,∠OBE的度数,继而求得答案.
解答 解:∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=4,∠OBE=60°,
∵OE⊥AB,
∴∠BOE=30°,
∵O为对角线BD的中点,
∴OB=$\frac{1}{2}$BD=2,
∴BE=$\frac{1}{2}$OB=1.
故选A.
点评 此题考查了菱形的性质以及等边三角形的判定与性质.注意证得△ABD是等边三角形是关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
15.将一次函数y=-2x+4的图象平移得到图象的函数关系式为y=-2x,则移动方法为( )
| A. | 向左平移4个单位 | B. | 向右平移4个单位 | C. | 向上平移4个单位 | D. | 向下平移4个单位 |
19.现有人数相等的甲、乙、丙三个旅行团,每个团旅客的平均年龄都是32岁,如果这三个团游客年龄的方差分别是S甲2=27,S乙2=19.6,S丙2=1.6,导游小王最喜欢带游客年龄相近的团队,则他应选( )
| A. | 甲团 | B. | 乙团 | C. | 丙团 | D. | 甲或乙团 |
16.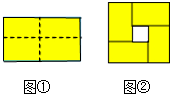 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )| A. | (m-n)2 | B. | (m+n)2 | C. | 2mn | D. | m2-n2 |

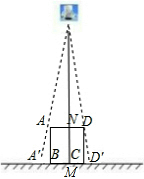 如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.
如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.