题目内容
1.明明家准备装修一幢大楼开宾馆.据调查,宾馆房间价定价为200元时,每天可租出50间,但每上涨10元,每天少租出1间,(1)房间定价为多少元时,每天的营业额达到12000元?
(2)房间定价为多少元时,每天的营业额最大?并求最大营业额.
(3)①对于问题(1),从节约成本角度来讲,你会建议明明装修多少间房间?
②对于问题(2),你又会建议明明装修多少间房间?
分析 (1)设房间定价为x元,则租出的房间数为(50-$\frac{x-200}{10}$),根据营业额=房间定价×租出的房间数列出方程解答即可;
(2)根据(1)中的基本数量关系列出二次函数,利用配方法求得最值即可;
(3)①从节约成本角度来讲,调高房价,求得答案;
②利用营业额的最大值,求得房价,得出答案.
解答 解:(1)设房间定价为x元时,每天的营业额达到12000元,
则:x(50-$\frac{x-200}{10}$)=12000,
解得:x1=300,x2=400,
答:房间定价为300或400元时,每天的营业额达到12000元;
(2)设每天的营业额为y元,则
y=x(50-$\frac{x-200}{10}$)
=-$\frac{1}{10}$x2+70x
=-$\frac{1}{10}$(x-350)2+12250
∵-$\frac{1}{10}$<0
∴当350时,y有最大值,且最大值为12250,
答:房间定价为350元时,每天的营业额最大为12250元;
(3)①从节约成本角度来讲,房价应高一点,
当x=400时,50-$\frac{x-200}{10}$=30(间)
答:建议明明装修30间房间;
②当x=350时,50-$\frac{x-200}{10}$=35(间)
答:从商家利润角度来讲,建议明明装修35间房间.
点评 此题考查二次函数的实际运用,理解每天的房间收费的两个因素:每间房实际定价、营业额y,与定价增加的关系,得出函数解析式解决问题.

 名校课堂系列答案
名校课堂系列答案| A. | 3 | B. | 6 | C. | 2$\sqrt{3}$ | D. | $\sqrt{6}$ |
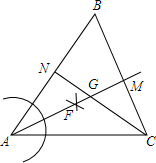 如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;
如图,在△ABC中,∠B=60°.以点A为圆心,任意长为半径画弧分别交AB、AC于点D、E,分别以点D、E为圆心,以大于$\frac{1}{2}$DE长为半径画弧,两弧相交于点F,作射线AF与BC相交于点M;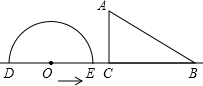 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的左侧,OC=8cm.(提示:直角三角形中,30度所对的直角边是斜边的一半,反之成立)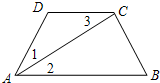 如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由.
如图已知∠1=∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由. 它的余角的度数是( )
它的余角的度数是( )