题目内容
 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:二次函数综合题
专题:压轴题
分析:求出直线AB与y轴的交点坐标,再求出∠ACP的余弦和正弦,过点D作DF⊥PC于F,设点P的横坐标为m,表示出PC,再利用∠ACP的余弦和正弦表示出DF,再表示出点B到PC的距离,然后根据PC分成的两个三角形的面积关系分两种情况列方程求出m,在待人抛物线求出横坐标,即可得解.
解答:解:令x=0,则y=1,
所以,直线y=
x+1与y轴的交点E的坐标为(0,1),
由勾股定理得,AE=
=
,
所以,cos∠ACP=
,
sin∠ACP=
,
过点D作DF⊥PC于F,设点P的横坐标为m,
则PC=
m+1-(
m2-
m-3)=-
m2+m+4,
所以,CD=PC•cos∠ACP=
(-
m2+m+4),
DF=CD•sin∠ACP=
×
(-
m2+m+4)=-
(m2-2m-8),
又∵点B到PC的距离为(4-m),
∴△PCD和△PCB的面积的比=-
(m2-2m-8):(4-m)=
,
当S△PCD:S△PCB=3:5时,
=
,
解得m=1,
此时,
m2-
m-3=
×12-
×1-3=-3,
点P的坐标为(1,-3),
当S△PCB:S△PCD=3:5时,
=
,
解得m=
,
∵
>4,
∴点P在点B的右边,不在直线AB的下方,不符合题意舍去,
综上所述,存在P(1,-3),使PC把△PDB分为的两个三角形面积之比为3:5.
所以,直线y=
| 1 |
| 2 |
由勾股定理得,AE=
| 22+12 |
| 5 |
所以,cos∠ACP=
| 1 | ||
|
sin∠ACP=
| 2 | ||
|
过点D作DF⊥PC于F,设点P的横坐标为m,

则PC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以,CD=PC•cos∠ACP=
| 1 | ||
|
| 1 |
| 2 |
DF=CD•sin∠ACP=
| 2 | ||
|
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 5 |
又∵点B到PC的距离为(4-m),
∴△PCD和△PCB的面积的比=-
| 1 |
| 5 |
| m+2 |
| 5 |
当S△PCD:S△PCB=3:5时,
| m+2 |
| 5 |
| 3 |
| 5 |
解得m=1,
此时,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点P的坐标为(1,-3),
当S△PCB:S△PCD=3:5时,
| m+2 |
| 5 |
| 5 |
| 3 |
解得m=
| 19 |
| 3 |
∵
| 19 |
| 3 |
∴点P在点B的右边,不在直线AB的下方,不符合题意舍去,
综上所述,存在P(1,-3),使PC把△PDB分为的两个三角形面积之比为3:5.
点评:本题是二次函数综合题型,主要利用了锐角三角函数的定义,三角形的面积,根据等底的三角形的面积的比等于高的比利用点B、D到AC的距离表示出两个三角形的面积的比是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果式子
+
有意义,那么点(x,y)在( )
| -3x |
| 1 | ||
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
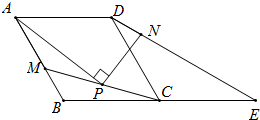 已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.
已知如图,四边形ABCD是菱形,∠ABC=120°,△DCE是等腰三角形,CD=CE,点B、C、E在一条直线上,点M是AB上的一点,P是线段MC的中点,PA⊥PN,点N在DE上.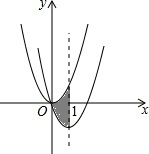 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两抛物线所围成的阴影部分的面积为( )
如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两抛物线所围成的阴影部分的面积为( )