题目内容
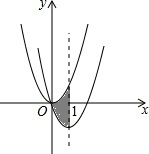 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两抛物线所围成的阴影部分的面积为( )
如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两抛物线所围成的阴影部分的面积为( )| A、2 | B、4 | C、8 | D、16 |
考点:二次函数图象与几何变换
专题:计算题
分析:先利用配方法得到抛物线y=x2-2x的顶点坐标为(1,-1),则抛物线y=x2向右平移1个单位,向下平移1个单位得到抛物线y=x2-2x,然后利用阴影部分的面积等于三角形面积进行计算.
解答:解:y=x2-2x=(x-1)2-1,即平移后抛物线的顶点坐标为(1,-1),
所以抛物线y=x2向右平移1个单位,向下平移1个单位得到抛物线y=x2-2x,
所以对称轴与两抛物线所围成的阴影部分的面积=
×1×2=1.
故答案为1.
所以抛物线y=x2向右平移1个单位,向下平移1个单位得到抛物线y=x2-2x,
所以对称轴与两抛物线所围成的阴影部分的面积=
| 1 |
| 2 |
故答案为1.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
已知一个Rt△的两直角边长分别为3和4,则斜边的平方是( )
| A、25 | B、14 | C、7 | D、5 |
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A、若AB∥CD,则∠3=∠4 |
| B、若AD∥BC,则∠3=∠4 |
| C、若∠1=∠2,则AB∥CD |
| D、若∠3=∠4,则AD∥BC |
 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y= 如图,一个无盖的长廊体盒子紧贴地面,一只蚂蚁由A出发,在盒子表面上爬到点G,已知,AB=7,BC=5,CG=5,求这只蚂蚁爬行的最短距离
如图,一个无盖的长廊体盒子紧贴地面,一只蚂蚁由A出发,在盒子表面上爬到点G,已知,AB=7,BC=5,CG=5,求这只蚂蚁爬行的最短距离 已知等腰△ABC中,AB=AC,D为AC的中点,且BD把△ABC的周长分成12和14两部分,求△ABC各边的长.
已知等腰△ABC中,AB=AC,D为AC的中点,且BD把△ABC的周长分成12和14两部分,求△ABC各边的长.