题目内容
6.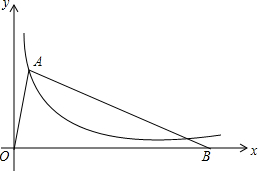 如图,点A在函数y=$\frac{5}{x}$(x>0)的图象上,点B在x轴的正半轴上,BO=BA,点A的横坐标为1.
如图,点A在函数y=$\frac{5}{x}$(x>0)的图象上,点B在x轴的正半轴上,BO=BA,点A的横坐标为1.(1)求点B的坐标;
(2)设C是AB的中点,D是线段OB上一动点,点A关于直线CD的对称点是A′.
①OD为何值时,点A′与点B重合?
②OD为何值时,以C,D,B,A′为顶点的四边形是平行四边形?
分析 (1)过点A作AH⊥OB于H,如图1,由点A的横坐标为1可求出OH、AH,设OB=x,则AB=OB=x,BH=x-1,然后在Rt△AHB中运用勾股定理即可解决问题;
(2)①设DB=m,则有AD=BD=m,HD=12-m,只需在Rt△AHD中运用勾股定理,就可解决问题;
②以C,D,B,A′为顶点的四边形是平行四边形并不唯一,可分两种情况进行讨论:Ⅰ.若BC是平行四边形的边,如图2,易证四边形CADA′是菱形,从而得到AD=AC=$\frac{13}{2}$,然后在Rt△AHD中运用勾股定理即可解决问题;Ⅱ.若BC是平行四边形的对角线,如图3,易得DB=CA′=CA=$\frac{13}{2}$,即可求出OD.
解答 解:(1)过点A作AH⊥OB于H,如图1.
∵点A在函数y=$\frac{5}{x}$(x>0)的图象上,xA=1,
∴OH=1,yA=$\frac{5}{1}$=5,
∴AH=5.
设OB=x,则有AB=OB=x,BH=x-1.
在Rt△AHB中,根据勾股定理可得:
52+(x-1)2=x2,
解得:x=13,
∴点B的坐标为(13,0);
(2)①若点A′与点B重合,如图1,
∵点A关于直线CD的对称点是A′,
∴DA=DA′=DB.
设DB=m,则有AD=BD=m,HD=12-m.
在Rt△AHD中,根据勾股定理可得:
52+(12-m)2=m2,
解得:m=$\frac{169}{24}$,
∴OD=OB-DB=13-$\frac{169}{24}$=$\frac{143}{24}$,
∴OD为$\frac{143}{24}$时,点A′与点B重合;
②Ⅰ.若BC为平行四边形的边,如图2,
则有四边形CDA′B是平行四边形,
∴DA′∥BC,DA′=BC.
∵点C是AB的中点,
∴AC=BC=$\frac{1}{2}$AB=$\frac{13}{2}$,
∴DA′∥AC,DA′=AC,
∴四边形CADA′是平行四边形.
∵DA=DA′,
∴平行四边形CADA′是菱形,
∴AD=AC=$\frac{13}{2}$,
∴HD2=AD2-AH2=$\frac{169}{4}$-25=$\frac{69}{4}$,
∴HD=$\frac{\sqrt{69}}{2}$,
∴OD=$\frac{\sqrt{69}}{2}$+1;
Ⅱ.若BC为平行四边形的对角线,如图3,
则有四边形CDBA′是平行四边形,
∴DB=CA′.
∵CA=CA′,
∴DB=AC=$\frac{13}{2}$,
∴OD=OB-DB=13-$\frac{13}{2}$=$\frac{13}{2}$.
综上所述:当OD为$\frac{\sqrt{69}}{2}$+1或$\frac{13}{2}$时,以C,D,B,A′为顶点的四边形是平行四边形.
点评 本题主要考查了反比例函数图象上点的坐标特征、平行四边形的性质、菱形的判定与性质、勾股定理、轴对称的性质等知识,证到四边形CADA′是菱形,从而得到AD=AC是解决第(2)①小题的关键.设某个线段为x,然后运用勾股定理(或相似三角形的性质或三角函数的定义)建立方程,并解出这个方程,是求线段长度常用的方法,应熟练掌握.另外,需要说明的是:当平行四边形的四个顶点的顺序不确定时,需分情况讨论.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{10}$ | C. | $\sqrt{(-2)^{2}}$=-2 | D. | $\frac{5}{\sqrt{5}}$=$\sqrt{5}$ |


 ,
,  ,
,  那么
那么 ,d三数的大小为( )
,d三数的大小为( ) B.
B.  C.
C.  D.
D. 
 将学生的两个三角板放成如图形状,若最短边长为1(即CD为1),求重叠部分△AEC的面积.
将学生的两个三角板放成如图形状,若最短边长为1(即CD为1),求重叠部分△AEC的面积.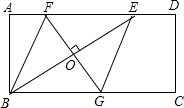 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{3}$AD,连接BE,作BE的垂直平分线分别交AD、BC于点F、G,FG与BE的交点为O,连接BF和EG.
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{3}$AD,连接BE,作BE的垂直平分线分别交AD、BC于点F、G,FG与BE的交点为O,连接BF和EG.