题目内容
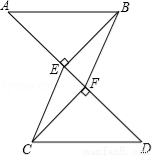
4．
将学生的两个三角板放成如图形状，若最短边长为1（即CD为1），求重叠部分△AEC的面积．
分析 先解直角△ACD，求出AC=$\sqrt{3}$，再作EF⊥AC于F，设EF=x，则AF=$\sqrt{3}$x，FC=x，根据AF+FC=AC列出方程$\sqrt{3}$x+x=$\sqrt{3}$，解方程求出x的值，进而得到△AEC的面积．
解答 
解：在直角△ACD中，∵∠ACD=90°，∠DAC=30°，CD=1，
∴AC=$\sqrt{3}$CD=$\sqrt{3}$．
作EF⊥AC于F，设EF=x，则AF=$\sqrt{3}$x，FC=x．
∵AF+FC=AC，
∴$\sqrt{3}$x+x=$\sqrt{3}$，
解得x=$\frac{3-\sqrt{3}}{2}$，
∴△AEC的面积=$\frac{1}{2}$AC•EF=$\frac{1}{2}$×$\sqrt{3}$×$\frac{3-\sqrt{3}}{2}$=$\frac{3\sqrt{3}-3}{4}$．
点评 本题考查了解直角三角形，三角形的面积，作出△AEC的高EF，设EF=x，根据AF+FC=AC列出关于x的方程是解题的关键．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
）
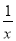，则
_______________．
如图，点A在函数y=$\frac{5}{x}$（x＞0）的图象上，点B在x轴的正半轴上，BO=BA，点A的横坐标为1．
定义：在平面直角坐标系xOy中，给定两点M（xM，yM），N（xN，yN），对于给定的实数a，b，作a|xM-xN|+b|yM-yN|为M，N的权重为a，b的直角距离，记为dxy（M，N），例如：d2，3（（1，0），（4，7））=2|1-4|+3|0-7|=27．