题目内容
11.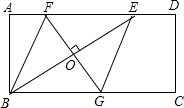 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{3}$AD,连接BE,作BE的垂直平分线分别交AD、BC于点F、G,FG与BE的交点为O,连接BF和EG.
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{3}$AD,连接BE,作BE的垂直平分线分别交AD、BC于点F、G,FG与BE的交点为O,连接BF和EG.(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数)时,求FG的长.
分析 (1)根据垂直平分线的性质求出OB=OE,BF=EF,根据矩形性质和平行线性质求出∠FEO=∠GBO,证△FOE≌△GOB,推出OF=OG,即可得出答案;
(2)求出AD=2a,DE=$\frac{2}{3}$a,AE=2a-$\frac{2}{3}$a=$\frac{4}{3}$a,根据勾股定理求出BE、求出OB,根据勾股定理求出BF,根据勾股定理求出OF即可.
解答 解:(1)四边形BFEG的形状是菱形,
理由是:∵BE的垂直平分线分别交AD、BC于点F、G,
∴OB=OE,BF=EF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FEO=∠GBO,
在△FOE和△GOB中,
$\left\{\begin{array}{l}{∠FEO=∠GBO}\\{OE=OB}\\{∠FOE=∠GOB}\end{array}\right.$,
∴△FOE≌△GOB,
∴OF=OG,
∵OB=OE,
∴四边形BFEG是平行四边形,
∵BF=EF,
∴四边形BFEG是菱形;
(2)∵AB=a,AD=2AB,DE=$\frac{1}{3}$AD,
∴AD=2a,DE=$\frac{2}{3}$a,
∴AE=2a-$\frac{2}{3}$a=$\frac{4}{3}$a,
∵四边形ABCD是矩形,
∴∠A=90°,
∵在Rt△ABE中,由勾股定理得:BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{a}^{2}+(\frac{4}{3}a)^{2}}$=$\frac{5}{3}$a,
∴BO=OE=$\frac{1}{2}$BE=$\frac{5}{6}$a,
在Rt△ABF中,由勾股定理得:AB2+AF2=BF2=EF2,
a2+($\frac{4}{3}$a-BF)2=BF2,
解得:BF=$\frac{25}{24}$a,
在Rt△FOB中,由勾股定理得:FO=$\sqrt{B{F}^{2}-B{O}^{2}}$=$\sqrt{(\frac{25}{24}a)^{2}-(\frac{5}{6}a)^{2}}$=$\frac{5}{8}$a,
∴FG=2FO=$\frac{5}{4}$a.
点评 本题考查了矩形的性质,垂直平分线性质,平行四边形的判定,勾股定理,菱形的判定的应用,能综合运用定理进行推理和计算是解此题的关键,综合性比较强,难度偏大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a2•a4=a8 | B. | 2a2+a2=3a4 | C. | 5a+3b=8ab | D. | (ab2)3=a3b6 |
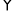 ABCD的对
ABCD的对 角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若
角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若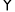 ABCD的周长为18cm,则
ABCD的周长为18cm,则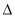 CDE的周长为__cm.
CDE的周长为__cm.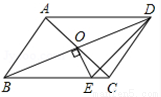
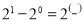 ,
,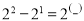 ,
, 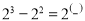 ,…
,…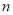 个等式,并说明第
个等式,并说明第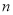 个等式成立:
个等式成立: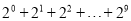 .
.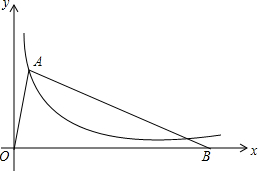 如图,点A在函数y=$\frac{5}{x}$(x>0)的图象上,点B在x轴的正半轴上,BO=BA,点A的横坐标为1.
如图,点A在函数y=$\frac{5}{x}$(x>0)的图象上,点B在x轴的正半轴上,BO=BA,点A的横坐标为1. 如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.
如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.